A Linean Cycle is not possible for a cube.

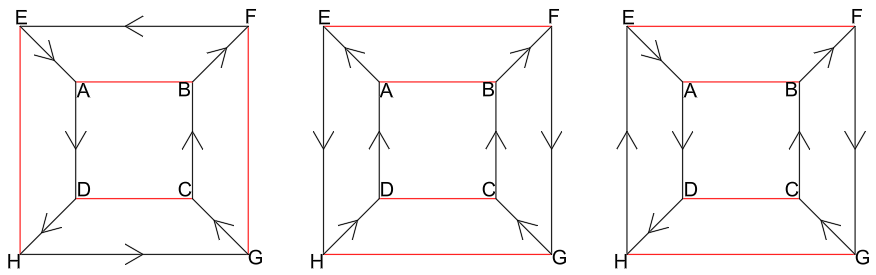
If we mark the doubly traversed edges in red, there are two distnict ways to colour the graph, and since at each vertex we arrive and depart, and since the red edges are responsible for net zero arrivals-departures, so must the black edges. Without loss of generality we can add directionality to the black edges such that they form a loop. A valid path must go red – black – red – black etc, since not doing so would result in a red edge being traversed consecutively. With one of the arrangements of red edges, the black edges form two smaller loops and so we must try them both going the same way, or going different ways.

In the first configuration, if we start with AB we go ABFGCDHE(AB…) completing a loop before all edges have been traversed.

Likewise in the second: ABFEHGCD(AB…), and the third: ABFE(AB…)

I’ll leave it for the reader to make a Linean cycle for the tetrahedron, dodecahedron or icosahedron.