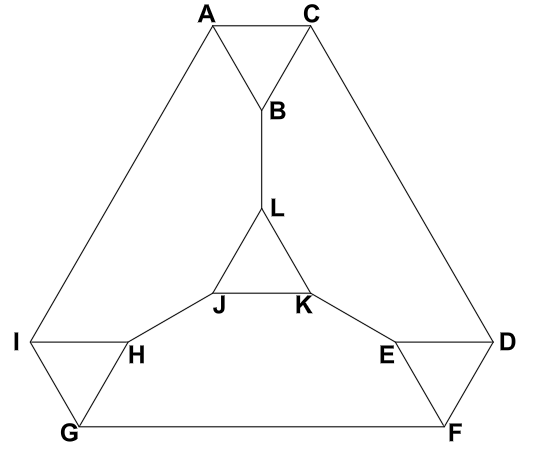
It is possible to run four of the repeated segments bidirectionally, and only incur penalty points on two paths. The network of paths is topologically equivalent to the edges of a truncated tetrahedron, and the same-direction repeated edges will be opposite edges of one of the hexagonal faces. That being the case the ‘cheapest’ edges to take the penalty points for are BL and HI, incurring only 5 penalty points in total.

The way to achieve this is A-C-B-L-J-K-E-D-C-A-B-L-K-J-H-I-G-F-D-E-F-G-H-I-A (or its reverse, or beginning at any other point in the cycle).