I deliberately drew the original diagram misleadingly so to not give the game away, but the fact that AB and CD are equal means that EF and GH are also equal, and that a line drawn between the centres of the top and right circles will be at 45 degrees downwards. It also follows that the line FG will be tangent to the top and right circles, and so will be equal in length to the line joining their centres. Since this is simply twice the unit radius, the length of FG will be 2.
Solution of the Week #302 - Five Triangles
Because of the symmetry of the set-up we are able to determine a few facts, irrespective of the particular shape of the triangle. We are able to assign areas A, B, C, D to different regions as shown. From the triangle SUY, A+B+C+D=1.
We can identify similar triangles PQR and PST, whose linear scaling is 1:2 and so whose area scaling is 1:4. So:
4B = A+2B+C
Similarly PUV has an area nine times that of PQR, so:
9B = 2A+2C+3B+2D
The first leads to 2B = A+C and the second leads to 3B = A+C+D, therefore B=D. Then, since B+D = A+C and all four add to 1, it follows that B and D are each equal to 1/4.
Next, look at similar triangles STX and QRW. The former is twice the linear scale, so four times the area of the latter, so:
C+D = 4C
3C = D
But we know that D=1/4, so C=1/12.
Since A+B+C+D=1, A = 1-1/4-1/12-1/4 = 5/12.
The area A is equal to five twelfths.
Solution of the Week #301 - Circular Table
Since every six consecutive friends adds to the same amount, it follow that 1-6 totals the same as 2-7, and since these two groups have five people in common it follows that 1 is the same age as 7. By the same reasoning, every person is the same age as the person 6 seats away. So 1, 7, 13 and 19 are all the same age. But the group (19,20,21,1,2,3) has the same total as (20,21,1,2,3,4), so 19 and 4 are the same age. Following this through the ages repeat in a pattern every three people, and each consecutive group of three people must add up to 100.
We are given the ages of 1 and 8 and asked for the age of 15. But 8 is the same age as 2, and 15 is the same age as 3, and together they will form a consecutive group of three adding to 100. If the first two are aged 25 and 33, the third must be aged 42.
The person seated at position 15 is aged 42.
Solution of the Week #300 - Winner Stays On
At first sight the question seems impossible. There is definitely not enough information to decide who plays who and when but, believe it or not, there in enough information to answer the particular question of who lost in the ninth game.
Firstly lets see how many games there were altogether. To do this we an simply add together the number of games played by each individual, and divide that total by two, since there are two players in each game. This tells us that there were 11 games in total. Because of the way they have of rotating players, even if a player loses, they will be back at the table three games later. The key now is to look at Billie, who has played the least games. If we assume they lost every game they played they would sill play roughly a third of the games. Say Billie played in game 1, they would play again in game 4, game 7 and game 10, but that is too many games. Similarly if they played and lost in game 2, they would reappear for game 5, game 8 and game 11. Still too many. The only possibility is that Billie played and lost in game 3, game 6 and game 9.
Billie lost in the ninth game.
Solution of the Week #299 - Change a Letter
CHEF CAME TO IT BUT NOT WISE AT BRAG AT OUR ASH AS FAST ONE
becomes:
THEF LAME TH AT BUR NST WICE AS BRIG HT BUR NSH AL FASL ONG
then:
THE FLAME THAT BURNS TWICE AS BRIGHT BURNS HALF AS LONG
Solution of the Week #298 - Unit Fractions
The numbers in the denominators are exactly those numbers that have either 2 or 5 or both as their prime factors, eg 8 = 2x2x2, 10=2x5. This is exactly the property which means they have a terminating decimal expansion.
You can organise the factions into a different order such that you first add those with no 5 factor at all:
A = (1 + 1/2 + 1/4 + 1/8 + 1/16 + …)
If you first double it:
2A = (2 + 1 + 1/2 + 1/4 + 1/8 + 1/16 + …)
And then you subtract the original:
A = 2
Next you look at those fractions which have exactly 1 factor of 5:
(1/5 + 1/10 + 1/20 + 1/40 + 1/80 + …)
You can factorise the 1/5 out of each term:
1/5 x (1 + 1/2 + 1/4 + 1/8 + 1/16 + …)
But that is just: 1/5 x A
The next group will be fractions with exactly 2 factors of 5, and similarly will total to 1/25 x A
The entire sequence will total:
AB, where B = (1 + 1/5 + 1/25 + 1/125 + …)
Multiply B by 5:
5B = (5 + 1 + 1/5 + 1/25 + 1/125 + …)
And subtract B:
4B = 5, so B = 5/4
The overall sum AB is therefore 2 x 5/4 = 5/2 = 2.5
Solution of the Week #297 - 2021 Puzzle
AB^4+CD^4 = 2021
AB^3+CD^3 = 485
AB^2+CD^2 = 101
AB+CD = 5
If you were to multiply one of the equations throughout by (B + D) you will get an equation involving some of the other terms on the left-hand side, along with BD and (B+D), for instance:
AB^3+CD^3 = 485, multiplied by (B+D):
1) AB^4+CD^4 + BD(AB^2+CD^2) = 485(B+D)
AB^2+CD^2 = 101, multiplied by (B+D):
2) AB^3+CD^3 + BD(AB+CD) = 101(B+D)
AB+CD = 5, multiplied by (B+D):
3) AB^2+CD^2 + BD(A+C)= 5(B+D)
In each of the equations let (B+D)=E and BD=F, and replace each of the ABCD terms with their numerical value, if known:
1) 2021 + 101F = 485E
2) 485 + 5F = 101E
3) 101 + (A+C)F = 5E
Multiplying 1) by 101 and 2) by 485 and subtracting one from the other gives an equation involving large numbers and F, but neatly divides to give F = 4. Plugging that back in to, say 2), gives a value of E = 5. Plugging both of these values into 3) gives a value of -19 for (A+C).
To find B and D we need to find a pair of numbers whose sum is 5 and whose product is 4. These must be 1 and 4. Let us assume for a moment that B is 4 and D is 1.
So we know that A+C is -19 and 4A+C is 5. Therefore A = 8 and C = -27.
(If we were to have assumed that B is 1 and D is 4, we would get A = -27 and C = 8, so the same four numbers but in a different order.)
Since we are asked for ABCD we get the same answer either way: -864.
Solution of the Week #296 - Three Hundred and Eighty Something
The more obvious solution is that 2 x 4 x 6 x 8 = 384.
The second is a little bit sneaky, as I didn’t specifically mention you could use negative numbers (as long as the result is positive): -7 x -1 x 5 x 11 = 385.
Solution of the Week #295 - Base 4 Code
Things work out best for those who make the best of the way things work out. John Wooden.
Solution of the Week #294 - Special K
The multiples of 11 will coincide whenever (K^2) – (4 x 5) is a multiple of 11. This occurs when K is either 3 more or 3 less than a multiple of 11, so 3, 8, 14, 19, 25, 30 etc.
The first three times this is a prime number are 3, 19 and 41.
Therefore the answer is 41.
For an explanation of why this is the case, read on:
Under the assumption that KM+5L and KL+4M are both congruent to 0, modulo 11, we can multiply either side by an integer and that congruence will be preserved. Therefore we can multiply the first expression by K (which is defined as an integer) and the second by 5. Therefore K^2.M+5LK and 5LK+20M are also both 0 mod 11.
Subtracting one expression from the other unifies the two expressions but maintains the divisibility by 11. Doing so makes the 5LK terms cancel out so we end up with (K^2 – 20)M is 0 mod 11. Therefore for our purposes, where we are interested in the special values of K, this occurs when K^2 – 20 is a multiple of 11, which is where we came in.
As a side note, if you’re wondering what happens if you follow the other strand and assume M is a multiple of 11, it’s not difficult to show that that means that L must also be a multiple of 11 for either/both of the original expressions to be a multiple of 11, which it will be for all K.
Solution of the Week #293 - Mental Calculation
Solution of the Week #292 - Base 4 Code
You can avoid reality, but you can't avoid the consequences of avoiding reality.
Solution of the Week #291 - Divisible by 32
n=2
Since 26 and 6 are both even, if n is greater than or equal to 5, both parts will independently be divisible by 32, so be only need to consider n = 1,2,3,4.
When n=1, it is obvious that 26+6=32.
When n=3, we note that (x^3 + y^3) can always be factorised into
(x+y)(x^2–xy+y^2), so letting x=26 and y=6 shows that this is divisible by 32.
When n=4, each part will be an odd number multiplied by 2^4, so will naturally have a remainder of 16 when divided by 32. Putting both of them together gives a multiple of 32.
That just leaves n=2. Unlike all of the other numbers, there is no inherent reason why this would be divisible by 32, and simply checking shows that it isn’t.
Solution of the Week #290 - Special Sequence
One possible answer is:
9 10 11 12 4 5 6 7 8 4 9 5 10 6 11 7 12 8
The structure hints at a general method (which might not have been apparent from the original example, but nevertheless follows the same idea). Using numbers m to n, n needs to be (at least) 3m.
If you’re interested I developed this into a sequence which has now been published on the OEIS (Online Encyclopedia of Integer Sequences): https://oeis.org/A338804
Solution of the Week #289 - Power Play
The remainder is zero. In fact 10^n + 11^n is divisible by 21 whenever n is an odd number.
You can prove this by showing that when n is odd, (a + b) is a factor of (a^n + b^n).
You can factorise (a^n + b^n) as:
(a + b)(a^(n-1) – a^(n-2)b + a^(n-3)b^2 - … - ab^(n-2) + b^(n-1))
When you multiply the massive second bracket by (a + b) almost everything cancels out, leaving only (a^n + b^n). Here is a specific example using n=5:
(a+b)(a^4 – a^3.b + a^2.b^2 – a.b^3 + b^4)
Multiplying each term in the second bracket first by a:
(a^5 – a^4.b + a^3.b^2 – a^2.b^3 + a.b^4)
And then by b:
(a^4.b – a^3.b^2 + a^2.b^3 – a.b^4 + b^5)
Adding those two brackets leaves only the first and last terms:
(a^5 + b^5)
So as long as a, b and n and integers, the whole second bracket will be too. Therefore (10 + 11) divides into (10^101 + 11^101).
Solution of the Week #288 - Round Table
There are 64 (2^6) possible gender permutations of the six children. For all the males to be seated together, all of the girls need to be older than all of the boys, and there is one such arrangement for each of the possible numbers of girls from 0 to 6, giving 7 possible valid arrangements.
Therefore the probability is 7/64, which is just under 11%.
Solution of the Week #287 - Divided Rectangle
Call the missing area x^2.
Let the base of the rectangle equal 2x/c (where x is positive, c is just an arbitrary scaling factor).
Since the area of a triangle is half base times height, the height of the missing triangle is xc.
Since the 4-triangle is similar to the missing triangle, the height of that is 2c (as 2^2=4), so the overall height of the rectangle is (xc+2c).
The area of the overall rectangle can now be written is two distinct ways, which must be equal:
Summing the four regions: x^2+15+4+26
Rectangle base times height: 2x^2+4x (notice the c vanishes)
Equating those two expressions and bringing everything to one side gives:
x^2+4x-45=0
which we can factorise into:
(x+9)(x-5)=0
The positive root is x=5, so the missing area x^2 is 25.
Solution of the Week #286 - The Cube and the Cup
To keep things relatively simple I will assume the circular rim of the cup has a radius of 1.
It’s not important to solving the question, but for the two orientations to be possible, the edge length of the cube must be somewhere between sqrt(6)/2 (1.225..) and 2. Any smaller than that and the point-down cube would fall in, any larger and the edge-down cube would not fit within the rim.
So on the assumption that we are within that range and both configurations are possible, it turns out that for the point-down orientation, the cube side length doesn’t matter: in theory you could have a mile long cube and the portion below the rim would be exactly the same.
To work out what that depth is for our unit radius cup, consider a cross-section through the cube and cup through point A O and D:
Since the entire face that triangle BCO is part of is perpendicular to edge AO, so is line OD. Projecting down to the side view we can use the fact that an angle in a semicircle is a right angle to ascertain that the depth is sqrt(2)/2 or 0.707…
So now we need to find the cube size for which the edge-down cube will also be at that same depth. By looking side-on at the diamond-shaped end of the cube with the required depth, and then looking at the plan view, we can see that the edge length of the cube must be sqrt(2) = 1.414…. Inevitably, this lies in our range of acceptable cube sizes.
So finally, how can you tell simply and visually if the edge length of the cube (as a ratio of the radius of the cup) exceeds sqrt(2)? Do you remember the forgotten third orientation – face-down? Simply if the face-down cube lies within the rim of the cup, then the ratio of edge length to radius is less than sqrt(2) and the edge-down orientation will be deeper than point-down, whereas if the face-down cube can sit on top of the cup with all four corners outside of the rim, then the point-down orientation will be deeper.
Solution of the Week #285 - Left Right Pairs
There are twelve different numbers in the list, so logically it can’t be done in fewer than 7 parts (3 of one hand and four of the other, to combine in 3 x 4 = 12 different ways).
However the fact that 23 is the only odd number in the list throws a spanner in the works as it effectively means one part will help make up the 23 but not be used elsewhere. Assuming that you can find a way of making the other 11 with just 3 + 4 distinct parts, 8 parts in total will be required.
If we assume for the moment that there are only 3 L parts, and that one of them has length 0 (impossible ultimately, but useful right now), then what we are searching for is a subset of four of the 11 lengths (so disregarding 23), and two number a and b such that the remaining 7 numbers can be made by adding either a or b to one of the 4 numbers.
By experimenting, the subset 20, 44, 48 and 50, with a and b values 8 and 26 fits the bill. To avoid the zero length part, we can simply subtract 10 from each of (20,44,48,50) and call those the L parts, and add 10 to (0,8,26) to find the R parts, adding in an extra R part to make 23 possible. Thus:
20 = 10L + 10R
23 = 10L + 13R
28 = 10L + 18R
44 = 34L + 10R
46 = 10L + 36R
48 = 38L + 10R
50 = 40L + 10R
52 = 34L + 18R
56 = 38L + 18R
58 = 40L + 18R
70 = 34L + 36R
74 = 38L + 36R
which uses the following eight parts: 10L, 34L, 38L, 40L, 10R, 13R, 18R, 36R.
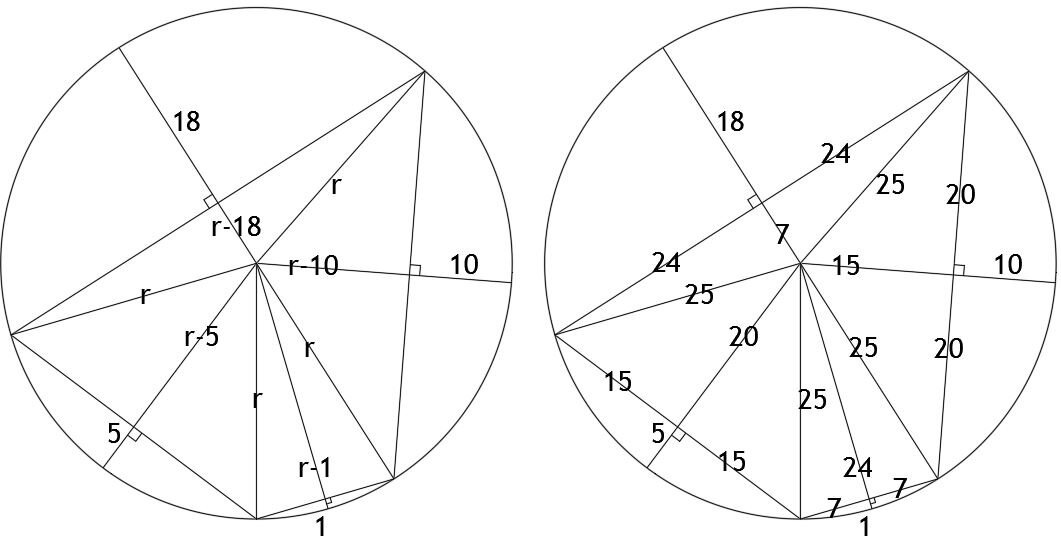
Solution of the Week #284 - Quadrilateral in a Circle
Area = 936.
To work through the problem in trigonometry is a bit of a nightmare so I’d envisage people solving the problem by drawing lines from all vertices and midpoints to the centre of the circle, calculating the cosine of each of the angles at the centre in terms of ‘r’, and then varying the value of r until the angles add up to 180 degrees. This occurs when r is precisely 25. From there we can easily work out the side lengths of all 8 of the internal right-angled triangles and tot up their areas to get 936.
If you do that you might be surprised to discover that the eight triangles are two sets of four congruent triangles: (7,24,25) and (15,20,25).