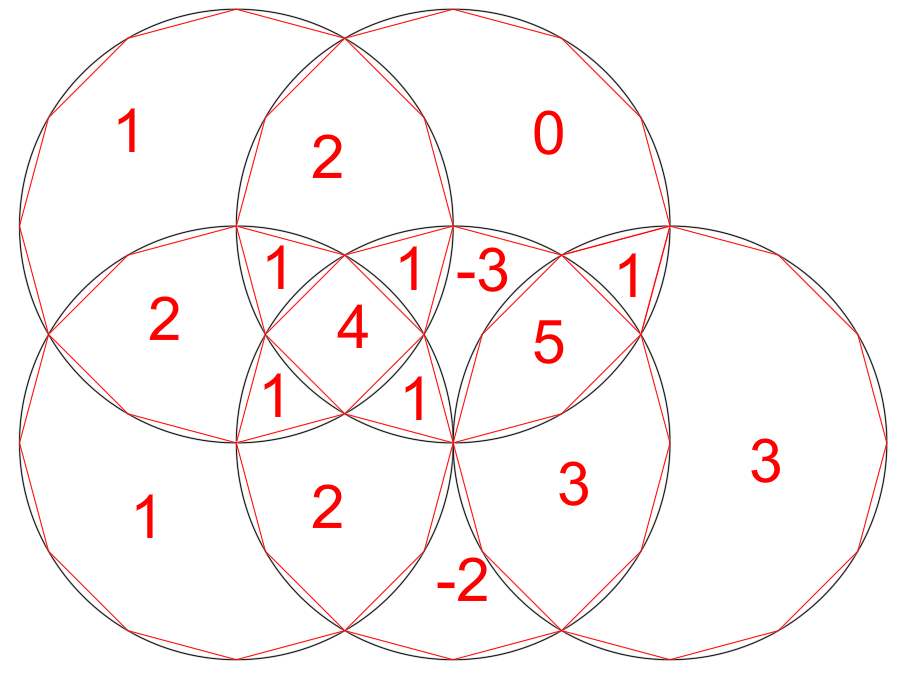
If we draw an inscribed dodecagon in each circle, then a necessary condition for the area being rational is that the number of convex borders is cancelled out by the number of concave borders. This is only the case for region C.

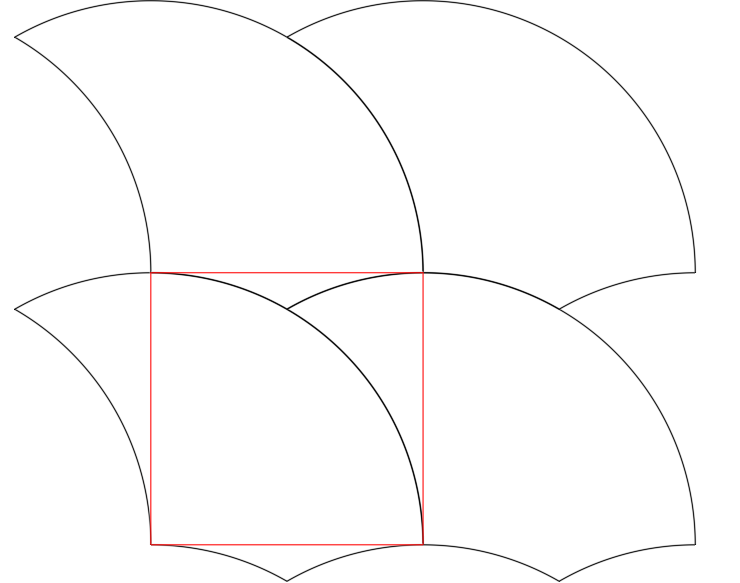
Region C has an area of exactly 1. You can verify this by tessellating the shape and overlaying a unit square:

Incidentally every area can be written as x*pi + y*sqrt(3) + z, where x, y and z are rational numbers. I had fun working them all out.