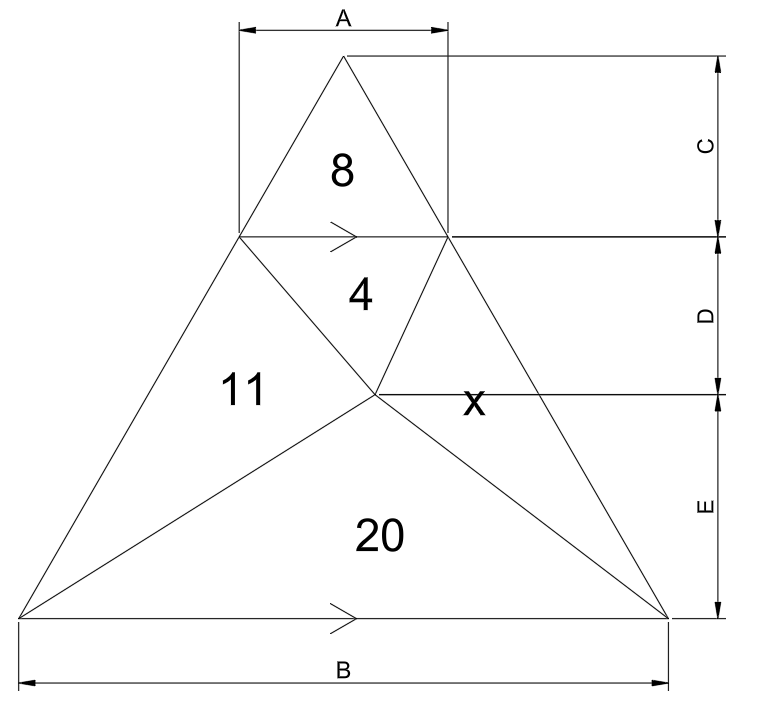
Since, if we find a valid figure we can scale it by ‘h’ in the horizontal and ‘1/h’ in the vertical to find any one of an infinite family of solutions, we can, without loss of generality, specify the particular figure where A = C. And since that top triangle of area 8 is similar to the figure as a whole we can also say that B = C+D+E.

A and C must both be equal to 4 to form the triangle of area 8. To form the triangle of area 4, D must equal 2.

From the triangle of area 20, B*E must be 40.

We know that B = C+D+E, and we also know the values of C and D, therefore E = B-6. So B*(B-6)=40. We could solve this as a quadratic, or else we can just look for two positive numbers 6 apart whose product is 40, namely 10 and 4.

So if B = 10, the entire figure has area 50, and if we subtract the known areas we find that area x = 7.

PS: If I wanted to be a little more general I would just multiply all of the horizontal lengths in the above solution by h and all the vertical distances by 1/h and when calculating the areas all hs would cancel.