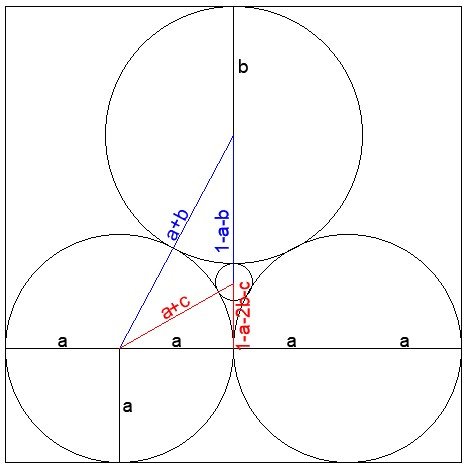
Let’s call the radius of the pair of identical circles ‘a’, the radius of the top circle ‘b’ and the radius of the small circle ‘c’ (the value we ultimately seek).

Since 4a = 1, a = 1/4.

Using Pythagoras on the blue triangle

(a+b)^2 = (1-a-b)^2 + a^2

a^2 + 2ab + b^2 = 1 – 2a – 2b + 2ab + a^2 + b^2 + a^2

2b = 1 – 2a + a^2

Substituting our known value of a = 1/4:

2b = 1 – 1/2 + 1/16

b = 9/32

Using Pythagoras on the red triangle:

(a+c)^2 = (1-a-2b-c)^2 + a^2

Let’s substitute our known values for a and b straight away:

(1/4+c)^2 = (3/16-c)^2 + 1/16

1/16 + c/2 + c^2 = 9/256 – 3c/8 + c^2 + 1/16

c(1/2+3/8) = 9/256

c = 9/256 * 8/7

c = 9/224