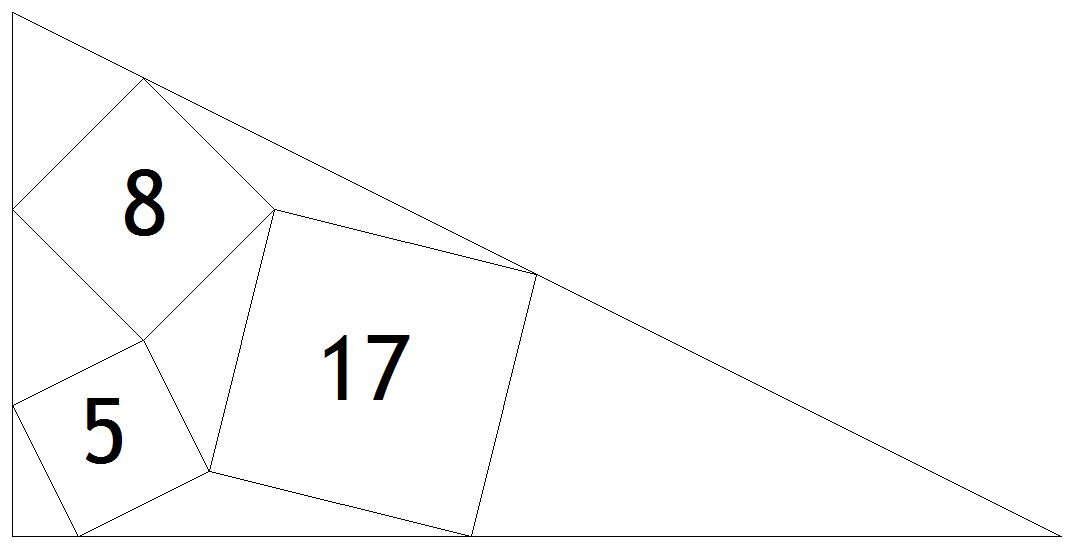
Three squares of area 5, 8 and 17 respectively, fit within a triangle as shown.
What is the area of the overall triangle?
Puzzle of the Week #254 - Three Squares in a Hexagon
Three squares fit in a hexagon as shown. The areas of the three squares are 200, 162 and 578 respectively.
What is the area of the entire hexagon?
Puzzle of the Week #253 - Build-a-Crossword
I have taken a completed crossword grid, removed all the consonants to the end of the row and/or column that they belong in, and then changed all the black squares into random vowels.
Your task is to reconstruct the crossword by figuring out which of the vowels are genuine and which need to become black squares, and by putting the consonants all back into place. Good luck!
Puzzle of the Week #252 - Hexagon Angle
Take a regular hexagon ABCDEF as below. Draw a line from A to a point midway between B and C, and another line from A to a point midway between D and F.
What is the angle between those two lines?
Puzzle of the Week #251 - Trispace
I have an equilateral triangle, dissected into three trapezoids and a smaller equilateral triangle. The PERIMETERS of the three trapezoids are 52, 66 and 80 respectively. The side length of the overall equilateral triangle (a) is precisely 13 times the side length of the smaller equilateral triangle (b).
What is the value of a?
Puzzle of the Week #250 - Squarespace
Four rectangles with areas as shown can be arranged to form a SQUARE with a SQUARE space left in the middle.
What is the area of the square space?
Puzzle of the Week #249 - Tetrahedron Packing
You have a tetrahedron-shaped space with a side length of 5 along each edge.
How many solid tetrahedrons of side length 1 can you fit into the space?
Puzzle of the Week #248 - Quartet
The four numbers 2,3,4 and 8 can be combined in pairs in six different ways, and the product of those six pairs will be
2 x 3 = 6
2 x 4 = 8
3 x 4 = 12
2 x 8 = 16
3 x 8 = 24
4 x 8 = 32
The sum of the original four numbers (2, 3, 4 and 8) is 17.
Can you find a different quartet of POSITIVE numbers whose products of pairs are also 6, 8, 12, 16, 24 and 32, but whose sum is less than 17?
Puzzle of the Week #247 - Diophantine Parallelogram
All of the lines on this diagram are integer lengths.
DE = 13
AD = BD
AB is parallel to CE
AC is parallel to BE
Angle CAD = angle DAB
What is the length of AD?
Puzzle of the Week #246 - Ghost Crossword
Use logic to fill in the crossword grid given only the clue numbers and the following rules:
1) The crossword is numbered in the usual way.
2) The grid is fully symmetrical.
3) The white area must all be connected together.
4) ‘Words’ are at least three letters long.
5) No 2x2 black squares are allowed.
6) No row or column is entirely white or entirely black.
Puzzle of the Week #245 - Three Digits
I have three digits A B C, such that A is less than B, which is less than C. I can arrange these to form six different 3-digit numbers.
When A is at the start, both possible numbers (ABC and ACB) are prime.
When A is in the middle, both numbers are semi-prime (the product of two prime numbers).
When A is at the end, the number is either abundant by 71 (the sum of its proper divisors is 71 more than the number itself), or deficient by 226 (the sum of its proper divisors is 226 less than the number itself).
What are the three digits?
Puzzle of the Week #244 - Three Way Split
Given a unit square it is possible to split it into three equal areas in a number of different ways. For instance cutting off the top third and then the bottom third. Or cutting off the top third then making a vertical cut to divide the remaining part in two. The total cut length of that first option is 2, whereas the total cut length of the second option is only 1+2/3.
Can you find a way of dividing the square into three equal areas, which requires even less total cut length?
Puzzle of the Week #243 - Shaded Circles
A circle of radius 2 has a circular hole of radius 1.
This is done is two alternative ways: in one the hole is tangent to the larger circle forming a crescent shape; in the other the hole is in the exact centre of the larger hole.
In the ‘crescent’ option a shaded circle of radius 1 is drawn, and then infinitely many smaller and smaller shaded circles are added heading off towards the two tips of the crescent.
In the ‘ring’ option just nine circles, each of radius ½ are drawn and shaded.
Which version has the largest combined shaded area?
Puzzle of the Week #242 - Where are they from?
If Jacob is from Edinburgh, Simon is from Sunderland, and Elliott is from Durham, where is Caroline from?
Puzzle of the Week #241 - Irregular Polyhedron
I have a polyhedron with the properties that every vertex is at the junction of exactly three faces, two of its faces are heptagons, and all its other faces are pentagonal.
How many pentagonal faces are there?
Puzzle of the Week #240 - Base 4 Code
I have written a sentence, and I have replaced each of the letters with the numbers that denote their position in the alphabet. However, I have used the base 4 number system.
Be careful, as some sequences of numbers could lead to several words, for instance 31110 could mean CAT (3,1,110), but could equally mean MAD (31,1,10).
1103 11311 11311 11311 12213210 11311 110211 3233110 3211110230121 1103 1132110311 1103 11311 20331001110 11033 2113333111.
Puzzle of the Week #239 - Nearly Equal Corners
A rectangle is split into four triangles as below. The areas of the three corner pieces are almost equal, with one being just 1 square unit larger than the other two. The remaining area is 1597 square units. What is the value of x?
Puzzle of the Week #238 - Circle Box
Here’s a fun challenge. The task is to fit circles into a grid according to the following rules:
· The centre of every circle must lie on a lattice-point of the grid, and no circles can share the same centre point.
· Every circle must have a whole number as its radius.
· The circles can touch each other and the edge of the grid, but cannot cross. In other words a circle can be entirely inside another, or entirely outside, but not partially inside.
· Your ‘score’ is the total area of all the circles you can fit in. A radius-1 circle has area of 1(pi), a radius-2 circle has an area of 4(pi), radius-3 = 9(pi), etc.
· The example 4 x 4 unit grid has a score of 6(pi) (4+1+1). I have marked the centre of each circle to show that none coincide.
What score can you achieve in the 12 x 12 unit grid?
Puzzle of the Week #237 - Right Angled Triangle Spiral
I have begun to construct a spiral of right-angles triangles thus:
The first triangle has legs both equal to 1.
Each subsequent triangle uses the hypotenuse of the previous triangle as one leg and a new line of length 1 as the other leg.
Every time the length of a spoke happens to be an exact whole number, I’ve marked it in red. I happened to notice that the angular distances between the red spokes are of a similar size.
My question is this: is it converging, and if so, to what?
Puzzle of the Week #236 - Zigzag
A zigzag of lines is drawn in a circle. The combined length of the three horizontal lines is exactly equal to the combined length of the two diagonal (parallel) lines. What is the angle formed between the horizontal and diagonal lines?
