Puzzle of the Week #234 - Split Squad
A junior football team has 15 players, with squad numbers from 1 to 15.
During training they split into two teams: a team of 7 and a team of 8, such that:
The sum of the squad numbers on team A is the same as the sum of the squad numbers on team B.
The sum of the squares of the squad numbers on team A is the same as the sum of the squares of the squad numbers on team B.
The sum of the cubes of the squad numbers on team A is the same as the sum of the cubes of the squad numbers on team B.
How was the squad split into the two teams?
Puzzle of the Week #233 - Simple but Complex
If x + y = 4, and x^2 + y^2 = 6, what are the values of x and y?
Puzzle of the Week #232 - Five Towns
There are five towns: Anderton, Barmby, Calderwood, Dempsey and Edinburgh.
There are straight roads between Anderton, Barmby and Calderwood.
Dempsey is exactly 25 miles from Anderton, Barmby and Calderwood.
Edinburgh is exactly 12 miles to the closest point on each of the roads between Anderton, Barmby and Calderwood.
How far is Dempsey from Edinburgh?
Puzzle of the Week #231 - Mastermind
You may be familiar with the game ‘Mastermind’, where one player forms a code of coloured pegs and another makes guesses. The coder tells the guesser after each guess how many pegs are fully correct, and how many others are present but in the wrong place.
My version is different from the standard version in three respects:
a) Instead of four, the code is now FIVE pegs long.
b) Instead of six different colours to choose from, in this version there are only TWO different colours of pegs: RED and YELLOW. There are therefore 2 to the power of 5, (32), different possible codes the coder might have set.
c) The guesser has decide what their first ‘n-1’ guesses are going to be straight away, before getting any feedback from the coder, such that when the feedback ultimately comes, the guesser can be certain of guessing correctly on the very next guess, the ‘nth’ guess (or earlier if one of the original n-1 guesses happened to have been correct). (In other words, if the guesser decides on 9 guesses and knows that whatever the code happens to be, they can use the feedback from those 9 guesses to be certain that the 10th guess will be correct, then n equals 10).
The question is then: what is the minimum value of ‘n’, such that the nth guess is guaranteed to be correct?
Puzzle of the Week #230 - Cairo-Word
I have taken a section of a Cairo tiling pattern and populated it with four-letter-words. To be helpful to you in your task of reconstructing it, I’ve given you both the list of words and the staring position and the direction of each of the words in the grid.
Puzzle of the Week #229 - Perfect Power Pairs
Most numbers cannot be expressed as a^b + c^d, where a and c are prime numbers and b and d are integers greater than 1. However there is one set of 6 consecutive numbers that all can, what are they?
Puzzle of the Week #228 - Ellipse
Below is a portion of an ellipse. The semi-minor axis has length 5. A 45 degree diagonal line from the centre to the edge of the ellipse has length 7.
What is the length of the semi-major axis?
If it helps, the general equation for an ellipse is:
(x/a)^2 + (y/b)^2 = 1, where a and b are the two semi-axes.
Puzzle of the Week #227 - Scrabble Ten-Pin Bowling
Here’s something a little different for you this week. This is a game I invented which you can play on your own or against others. All you need is a bag of tiles from a standard Scrabble set. Randomly draw out ten tiles and arrange them in a triangle. This is the first frame of the game of ten-pin bowling. If you can form a ten-letter word, you have scored a strike. If you can form two words using each of the ten letters exactly once each, this is a spare. If you can do neither, try to use as many letters as possible in at most two words. Scoring is exactly the same as for ten-pin bowling. Continue for all ten frames (there are 100 letters in a scrabble set), and then tot up your score.
If you’re not familiar with the scoring system of ten-pin bowling I’ll briefly explain: you get points for each word, equal to how many letters in the word. In addition, if you get a spare (use all letters in one frame using two words), you get bonus points equal to the next word you score.
If you get a strike (a ten letter word), you get bonus points equal to the next two words you score.
If you only get one word in a frame, and it's not a strike, then for the purposes of bonus points, you get a zero length word too.
In real tenpin bowling, if you get a strike or a spare on the tenth frame, you get an eleventh frame to determine your bonus points, and if you were lucky enough to get a strike on the tenth and eleventh frames, you would get a twelfth frame.
In this game, there are no eleventh and twelfth frame, so to determine any bonus points you are entitled to after the tenth frame, look back at the words you scored in the first and second frames.
So that’s the general outline of the game. For the purposes of this Puzzle of the Week I’ve randomly generated a complete game. Try to resist using solving tools as it takes the fun out of it, and see what the highest score you can achieve by only spending a minute on each frame.
For reference I scored a modest 95 points. But then this is a particularly tough board! I don’t believe there are any strikes up for grabs (prove me wrong!), but a spare is possible on at least some of the frames.
Puzzle of the Week #226 - Crazy Currency
In Elbonia they only have three denominations of coins: 15 ELB, 21 ELB and 35 ELB. Although each pair of these coins have a common factor, all three do not. This means that if the value is high enough, any value can be expressed exactly with no change required. But what is the highest amount that cannot be expressed exactly?
Puzzle of the Week #225 - Six Integers
x^2 = a^2 + 4b + 1
y^2 = b^2 + 4c + 1
z^2 = c^2 + 4a + 1
a, b, c, x, y, z are all positive integers
a > b > c
x > y > z
What are the values of the six integers?
(There is a really neat algebraic trick you can use here. First see if you can calculate x in terms of a).
Puzzle of the Week #224 - How Many Coins
I have a number of coins. I throw them all, count how many heads and how many tails and multiply those two numbers together. I calculate what the expected (average) answer should be and discover it is exactly three times the number of coins. How many coins do I have?
(For instance if there were three coins, there are eight possibilities:
HHH TTT HHT HTH THH TTH THT HTT
The first two result in 3 x 0 = 0, and the other six result in 2 x 1 = 2, so the average answer is 1.5)
Puzzle of the Week #223 - Winston Churchill
I have a six letter word, a clue to which is: ‘Something Winston Churchill often is’.
If I change the first letter of my word to the letter that follows it in the alphabet, and then reverse the entire word, I get a new word.
What was my word?
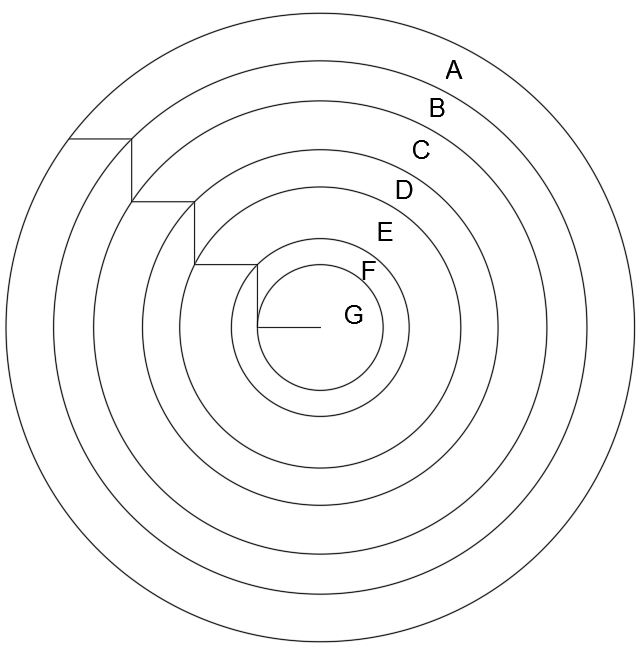
Puzzle of the Week #222 - Staircase Rings
In the following diagram, the ‘staircase’ is made up of horizontal and vertical lines of equal length. The ends of these lines determine the radius of each of the rings, whose shared centre is the end of the final horizontal line.
If the overall shape has an area of 100, what is the area of each of the individual regions A to G?
Puzzle of the Week #221 - Quotation Wordsearch
A quotation has been hidden in the large grid below. The first word can be read off (left, right, up, down, but not diagonally), and its letters eliminated. Later words in the quotation may not be made of consecutive letters until the letters of previous words have been eliminated. All the letters in the grid will be used exactly once then eliminated.
As an example, the phrase ‘In the nick of time’ has been hidden in the example grid:
“4, 3, 6, 3, 8: 3, 8, 3, 5, 9. 3, 2, 3, 4, 5, 3, 6”
Puzzle of the Week #220 - 23 Days
If we count a workday as a day that is not Saturday or Sunday and is not a Bank Holiday, the most you will see in a given calendar month is 23. This happens twice in 2019: July and October. In the UK there are Bank Holidays at New Year, Easter, May, August and Christmas. Is it possible for a calendar year to have no months with 23 workdays?
Puzzle of the Week #219 - Four Leaf Clover
Four identical pieces forming a square with a four-leaf-clover shaped hole can be rearranged (after flipping half the pieces) into a rhombus with three circular holes. The shorter diagonal of the rhombus is the same as the side length of the square.
Rounded to the nearest whole number percentage, what proportion of the square is shaded?
Puzzle of the Week #218 - Fast Flowing River
Grace and Ruby live in a house next to a fast flowing river. One day they decide to travel a few miles down the river and then return home. Grace is on foot, jogging along the riverbank at a speed of 5mph. Ruby takes the boat, which can travel at 9mph relative to the current of the river. They both set off at the same time, turn around at the same spot and arrive home at the same time. How fast was the current of the river?
Puzzle of the Week #217 - Identical Twins
Phyllis and Dilys are identical twins. They are each independently given the same 4-digit number.
Phyllis takes the number and converts it from decimal (base 10) to base 4, and writes down the 6-digit result.
Dilys simply writes the first and last digits of the number followed by the number in its entirety.
They are astonished to find that they have both written down the same 6-digit number!
What was the original number?
In other words, which number ABCD, when converted from decimal to base 4 becomes ADABCD?
Puzzle of the Week #216 - Four Semicircles in a Rectangle
Four semicircles are arranged around the edges of a rectangle. What are their respective radii?
This is a great deal more difficult than ‘Three Semicircles in a Square’. If it helps I can tell you that there is exactly one solution, and that each of the radii are rational numbers (so if you find it useful – and I’m not at all sure you will - you can scale the whole thing up by some factor, solve as a Diophantine set of equations, and scale back down again). I myself found this very difficult to solve, so if you discover a route to the solution that is not too difficult, I would be interested in knowing it.