Three semicircles are arranged around the edges of a unit square. What are their respective radii?
Puzzle of the Week #214 - Travelling Salesman
A travelling salesman needs to visit each of the black squares in turn and return to where he started. He can choose to start wherever he wishes. He traces a zero-thickness path, can travel at any angle (this gridlines are only a reference) and doesn’t need to go to the middle of each black square, it is sufficient for his route to touch a corner or an edge. If each small square measures 1 x 1, what is the length of the shortest route?
Puzzle of the Week #213 - Collate
Given a string with three each of three different letters ordered thus:
A A A B B B C C C
It is possible through a series of three moves to change the order into:
A B C A B C A B C
A ‘move’ consists of taking a section of the string and reversing the order of the items within it. The brackets show the section to be reversed in the subsequent move:
A(AABB)BCCC -> ABBA(ABC)CC -> AB(BACBAC)C -> ABCABCABC
Using the exact same idea, how many moves will it take to change between the following?
A A A A A B B B B B C C C C C D D D D D E E E E E
A B C D E A B C D E A B C D E A B C D E A B C D E
Puzzle of the Week # 212 - Infinite Sum
The convergent sum of the following infinite sequence, in its simplest terms, is a fraction with a square number on the top and a factorial number below.
1/7 + 1/16 + 1/27 + 1/40 + 1/55 + 1/72 + … + 1/n(n+6) + …
What is it?
Footnote: the partial sum converges extremely slowly, such that if you add the first million terms you will only get the first 5 decimal places. However there exists a very nice trick to allow you to work out exactly the number the infinite sum converges upon (without having to do an infinite number of calculations!).
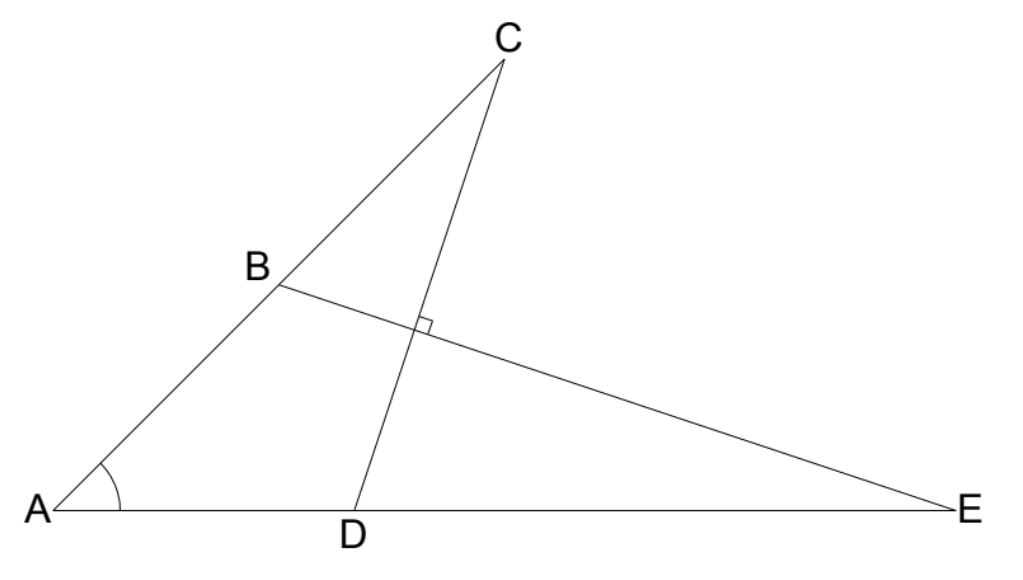
Puzzle of the Week #211 - Angle
B is the midpoint of AC
D is one third of the way along AE
CD is perpendicular to BE
AE is (√2) times the length of AC
What is the angle at A?
Puzzle of the Week #210 - Return Journey
The towns of Abbottsville, Beresford and Christchurch all lie on one straight road. I embark on a journey from Abbottsville, through Beresford, to Christchurch, and back the same way. Each day I cover 1 mile more than the day before. It takes me 10 days to travel from Abbottsville to Beresford, 11 days to travel from Beresford to Christchurch and 12 days to travel from Christchurch (through Beresford) to Abbottsville.
What are the distances between the towns?
Paddocks App News!
The open beta has now started 🎉
Also, there’s now a little trailer on the store page (link to the trailer: https://www.youtube.com/watch?v=is8n293Z_zs).
Unfortunately, Google doesn’t offer Instant Apps for beta versions, so at the moment there is no free
demo available. We can hopefully get that sorted in the next few days.
Moritz Neikes has done a tremendous job with the app, thank you Moritz!
Puzzle of the Week #209 - Coin vs Dice
Which of the following scenarios should on average* take the most throws:
Repeatedly tossing a coin until you have seen at least 6 heads and at least 6 tails, or
Repeatedly throwing a dice until you have seen each of the numbers 1 to 6 at least once each?
*(simple arithmetic mean)
Puzzle of the Week #208 - Factorials Again!
Find a set of three (different positive whole) numbers whose sum is 6! And whose product is 9!
Puzzle of the Week #207 - Factorials
Find a set of four different positive whole numbers whose sum is a factorial number and whose product is also a factorial number.
Puzzle of the Week #206 - Tumbler
A glass tumbler has an outside diameter of 78mm, and inside diameter of 72mm and a solid base that is 30mm deep.
Its centre of gravity is exactly 30mm from the table, ie, at the height of the bottom of the inside of the glass.
What is the overall height of the glass tumbler?
Puzzle of the Week #205 - Formula
I have a sequence. It begins:
1
101
10101
1010101
101010101
etc
As it’s populated entirely with 1s and 0s it is not entirely clear whether these are decimal numbers, or binary numbers, or some other base entirely.
Construct a formula to give the nth term, which works no matter what base we are working in.
***EDIT*** You are looking for a simple formula where you plug in the value of n and get the nth term, no recursive formulae or finite sums required.
Puzzle of the Week #204 - Region Sandwich
I’ve taken the name of a particular sub-national region of a large country and split it apart. It is possible to use each of the following as a filling in the ‘sandwich’ to create three words:
_____R_____
_____CH_____
_____INL_____
What is the name of the region?
Puzzle of the Week #203 - Fractions
1/3 = 0.333… and 3/8 = 0.375. No fraction with a single-digit denominator lies between them.
What is the fraction greater than 1/3 and less than 3/8 that has the lowest denominator? Call that fraction ‘x’.
What is the fraction greater than ‘x’ and less than 3/8 that has the lowest denominator? Call that fraction ‘y’.
Finally, what is the fraction greater than ‘x’ and less than ‘y’ that has the lowest denominator?
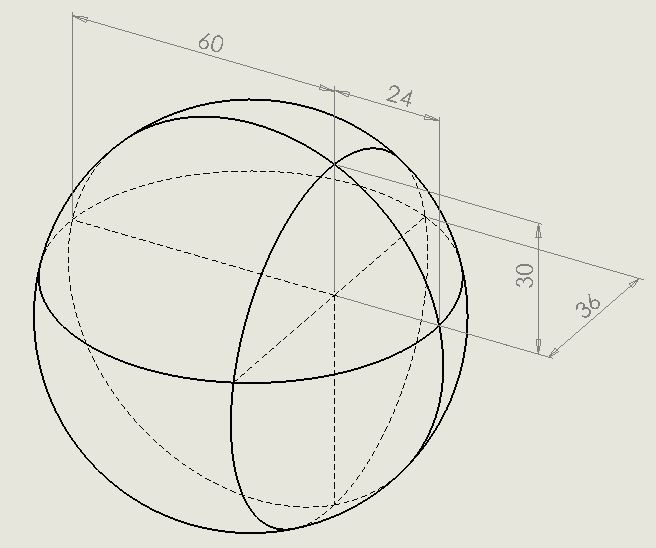
Puzzle of the Week #202 - Spherical Asteroid
A perfectly spherical asteroid is in orbit somewhere in the solar system. There is a small deposit of Unobtainium buried within it.
Scientists are able to scan the asteroid and determine the position of the deposit of Unobtainium relative to the surface of the sphere, by imposing a perpendicular coordinate system on it:
From the Unobtainium, if you go the 24 metres in the positive x direction you reach the surface
From the Unobtainium, if you go the 60 metres in the negative x direction you reach the surface
From the Unobtainium, if you go the 30 metres in the positive y direction you reach the surface
From the Unobtainium, if you go the 36 metres in the positive z direction you reach the surface
What is the radius of the spherical asteroid?
This may help you: The general equation of a sphere is: (x - a)² + (y - b)² + (z - c)² = r², where (a, b, c) represents the centre of the sphere, r represents the radius, and x, y, and z are the coordinates of the points on the surface of the sphere.
Puzzle of the Week #201 - Two of One and One of Another
I recently investigated which numbers can be represented at the sum of one square number and double a different square number, for instance 9 is 1+2(4), or 38 is 36+2(1).
With pencil and paper: 99 is the smallest number that can be represented as a^2 + 2b^2 in three different ways: find them all!
With a computer: what is the smallest number that can be represented as a^2 + 2b^2 (with a and b different positive integers) in six different ways?
Puzzle of the Week #200 - Mental Arithmetic
Puzzle of the Week #199 - Double Digiproduct
I have a number.
I multiply each of the digits together to get another number.
I multiply each of the digits of that number together, and I find that I get the number 36.
If you disallow the use of the digit 1 (for obvious reasons) there are only two numbers I could have started with, what are they?
Puzzle of the Week #198 - 123 456 789
Which is greater:
the 789th number in the 123 times table to begin with the digits 456,
or the 123rd number in the 789 times table to begin with the digits 456?
Puzzle of the Week #197 - Volcano Climb
An expedition is being planned to climb a truncated conical volcano that is 40km diameter at the base, and 24km diameter at the crater edge. The slope length is 12km.
The path starts at A at the base and ends at point B on the crater edge, exactly halfway round the volcano from A.
What is the length of the shortest possible route around the conical face of the volcano (to the nearest km)?