Puzzle of the Week #189 - Three Palindromes
I recently stumbled upon an intriguing theorem that stated that every positive whole number can be expressed as the sum of three palindromic numbers, although it is often far from straightforward to find them.
Can you express the number 6878592 as the sum of three palindromes?
It is the sum of three numbers of 7, 6 and 5 digits respectively, and no digit is repeated except where being a palindrome dictates it:
ABCDCBA + EFGGFE + HJKJH = 6878592
Puzzle of the Week #188 - Triple Indivisibility
We have a whole number, let’s call it ‘b’.
We also have a number of statements:
1 divides exactly into ‘b’
2 divides exactly into ‘b’
3 divides exactly into ‘b’
4 divides exactly into ‘b’
… continuing all the way to …
‘a’ divides exactly into ‘b’
We are told that three consecutive statements in the list are NOT true, while all of the others are true.
Question a: what is the MAXIMUM value that ‘a’ could possibly be?
Question b: given that value for ‘a’, what is the MINIMUM value that ‘b’ could possibly be?
Puzzle of the Week #187 - Wasteful Process
An industrial process needs 7kg of material to produce one widget, but in doing so produces 2kg of waste material which can then go towards making another widget.
If I start with 4937kg of material, how many widgets can I make altogether?
Puzzle of the Week #186 - Prime of my Life
I celebrated my birthday this week. Right now, my age, and those of my wife, my daughter and my son, are all prime numbers. After my daughter celebrates her next birthday in a few months we will not all be prime ages until 30 years from now. And after that (if we are all still around) it would be another 30 years.
My daughter is about four and a half years older than my son, and I am about one and a half years older than my wife. How old are we all?
Puzzle of the Week #185 - How Long is a Piece of String?
I have a loop of string N centimetres long. I can form this loop into a square with n cm along each side (n being exactly a quarter of N). Not surprisingly I find that if I draw diagonals from opposite corners of this square, they cross at right angles. I also find that I can tilt the square into a rhombus shape, while still having n cm along each side, the diagonals still cross at right angles. Still not surprising.
However, I discover that if I move some of the corners so that instead of all being n cm long, the four edges of the quadrilateral are n, n-5, n+1 and n+4, then the diagonals STILL cross at right angles.
How long in my loop of string?
Puzzle of the Week #184 - Random Code
Replace each letter in this code either by the letter preceding it or following it in the alphabet.
ITLJMJUZ JR ONU SGJOJJOF KDRR NG XPTQRFMG ATS SIHOJJOH PG ZPVQRDKE MDTR
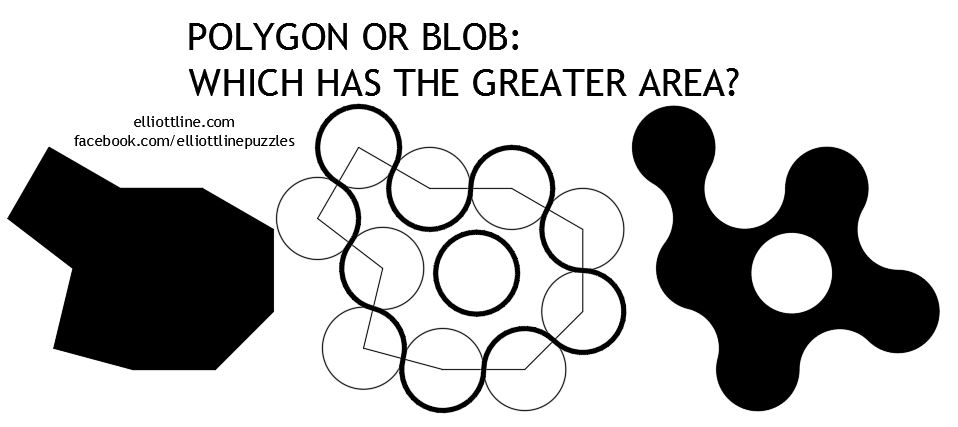
Bonus Puzzle - Polyblob
Puzzle of the Week #183 - Seven Digits
Find the seven digits A, B, C, D, E, F and G such that ABCDEF divided by G = GFEDCB.A
Puzzle of the Week #182 - The Rickety Carousel
There is a rickety old carousel, with 24 horses equally spaced around the edge of a disc. There are at least two things wrong with it: one is that the horses in positions A, B, C, D, E, F and G are broken and not safe to ride; another is that the carousel needs to be perfectly balanced around the centre of the disc, otherwise it won’t go round. This means that when there are two children wishing to ride, they would have to be positioned in diametrically opposite positions, eg, A and M, in order that the centre of gravity is at the centre of the disc. If there were three children they could be at positions A, I and Q.
On this particular day, nine children wish to ride the carousel. Where do they need to be positioned such that the centre of gravity is at the centre of the disc, and that positions A to G are unoccupied?
Puzzle of the Week #181 - Number Hunt: Four Digit Product
Find a four digit number ABCD such that ABCD x ABC x AB x A = 369,457,740
Bonus Puzzle - Merge In Turn
Bonus Puzzle - Ladders in the Alleyway
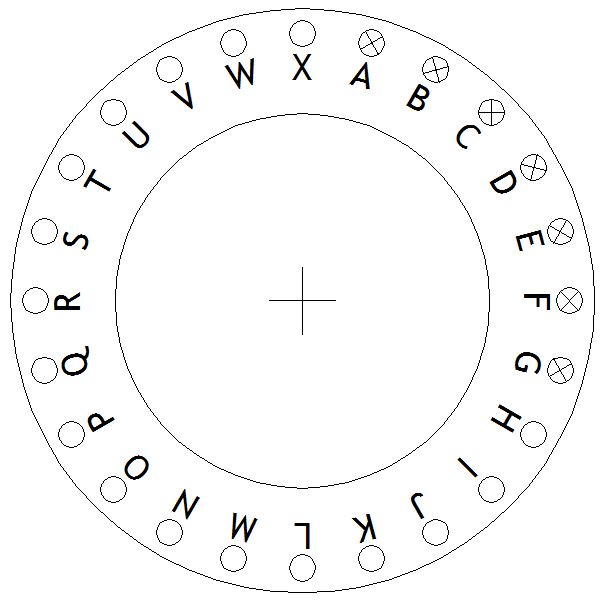
Puzzle of the Week #180 - Letter Wall
Two letters of the alphabet are chosen at random. What is the probability that the bricks that correspond to those letters are adjacent in this wall:
Puzzle of the Week #179 - Reducing the Irreducible
The fraction 1174/5063 cannot be reduced further in the usual way, however it can be expressed exactly using only six digits instead of eight.
How?
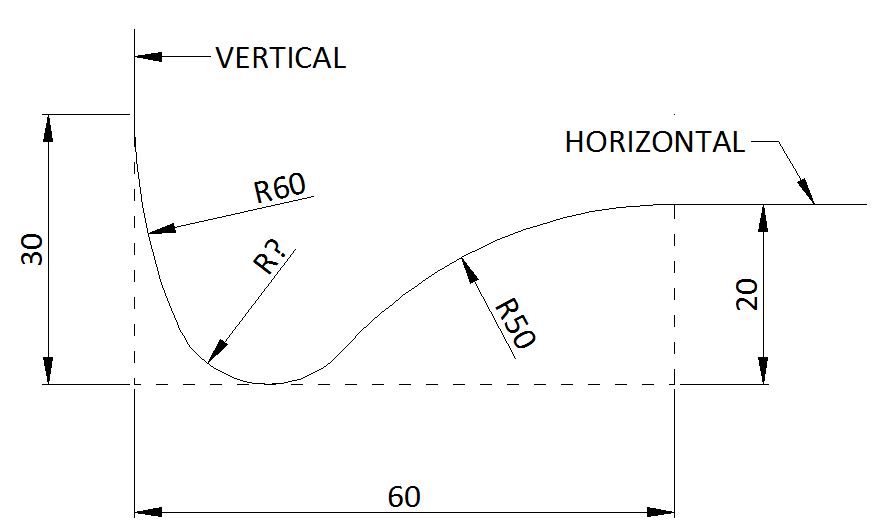
Puzzle of the Week #178 - Tangent Curve
The line begins in a vertical downward direction, transitions into an arc of radius 60, then into another arc with a tighter radius, which just touches the horizontal dashed line. Then there is an arc of radius 50 in a clockwise direction, then a horizontal line. At each transition between line and arc or arc and arc the tangents are continuous.
What is the missing radius?
Puzzle of the Week #177 - Skyscrapers and Empty Lots
Each of the 25 squares contains either a building of height 1, 2, 3 or 4, or an empty lot. Each row and each column contains exactly one of each of those.
The numbers in the twenty ‘vantage points’ around the edge denote how many buildings you can see looking along that particular row or column, so for instance if the 2 building was closest, followed by 1, 4 and 3 in that order, the vantage point would say 2, as you can see the 2-building and the 4-building, whereas the 1-building and 3-building are hidden behind taller buildings.
Here’s an example (with only 1, 2 and 3 height buildings) which might make it clearer, followed by the puzzle itself:
Puzzle of the Week #176 - Nine Point Circle
You might be familiar with the famous ‘Nine Point Circle’ theorem, which says that for ANY triangle the 3 midpoints (shown below in red), the 3 perpendicular feet (shown in green), and the 3 points midway between the each of the vertices and the orthocentre (shown in blue), will all lie on a circle. (Of course for an equilateral or isosceles triangle some of these points will coincide). But I have discovered there is something quite special about the 9 points of a triangle with angles 45, 60 and 75.
What is so special?
The figure is to scale so you may be able to guess the answer.
Puzzle of the Week #175 - Out Standing In My Field
I’m standing in a rectangular field. I am 34m from the top left corner and 62m from the bottom right corner. I am an equal distance from the other two corners: what is that equal distance?
Puzzle of the Week #174 - Rectangle Area
The AREA of each of the eight squares is 26. What is the area of the rectangle that surrounds them?