I happen to look at the clock and notice that the angle between the hour hand and the minute hand is precisely 90 degrees.
How long, to the nearest second, until the angle between the hands is again 90 degrees?
Your Custom Text Here
I happen to look at the clock and notice that the angle between the hour hand and the minute hand is precisely 90 degrees.
How long, to the nearest second, until the angle between the hands is again 90 degrees?
I’ve introduced a couple of refinements to my Binary Determination puzzle: firstly roughly equal amounts of ones and zeros (previously there were more ones at a ratio of about 2:1); secondly a more concise way of giving the solution
Place a 0 or 1 in each of the empty cells so that in each row and column a pair of 5-digit binary numbers can be read (therefore with decimal values between 0 and 31), such that the product of the two numbers in a particular row or column is shown at the end of that row or column.
Here is an example (using only 3-digit binary numbers), so for instance in the first column, 010 (2) multiplied by 011 (3) is equal to 6, (as there is a 6 at the foot of the first column) and similarly for all of the other columns and rows. Finally, read off the diagonal of each quarter of the grid and convert back into decimal to give the solution (3,3,2,3):

Here is the puzzle:

Here’s a brand new type of puzzle that I’ve just invented this week.
Place a 0 or 1 in each of the empty cells so that in each row and column a pair of 5-digit binary numbers can be read (therefore with decimal values between 0 and 31), such that the product of the two numbers in a particular row or column is shown at the end of that row or column.
Here is an example (using only 3-digit binary numbers), so for instance in the first column, 010 (2) multiplied by 011 (3) is equal to 6 (as that is the number at the foot of the first column), and similarly for all of the other columns and rows.

Here is the puzzle:

Imagine two games:
In one a person rolls a dice repeatedly and notes down the result. If a particular number appears three times, any subsequent roll of that number will be ignored. This is continued until ten numbers have been written down.
In another there is a pack of 18 cards, three each with the numbers 1 to 6 on them. 10 cards are drawn at random. The ten numbers are written down.
In both cases the result will be ten numbers between 1 and 6, with no number appearing more than three times. It will be impossible to know whether the ten numbers came from the dice or the cards.
Is it possible to detect, given the results of many repeated trials, which game someone is playing, or are the two games essentially identical? (I’m not for numbers, just general trends that one might look out for).
I know, I know, the printing and postage costs of print-on-demand are not inconsiderable, and whilst I believe Paddocks is better appreciated in its pocket size printed book form, I have now decided to make it available as an ebook.
Not only is it cheaper than the printed book (even with its 40% discount), but also you don't need to pay postage, and it is delivered immediately.
So what's stopping you accessing more than 100 great puzzles (mostly Paddocks, but some other interesting and novel varieties too)?
http://www.lulu.com/shop/elliott-line/paddocks/ebook/product-23381678.html
How many different ways are there of arranging the letters of ENIGMATIST, such that no two vowels are adjacent, and no two identical letters are adjacent?
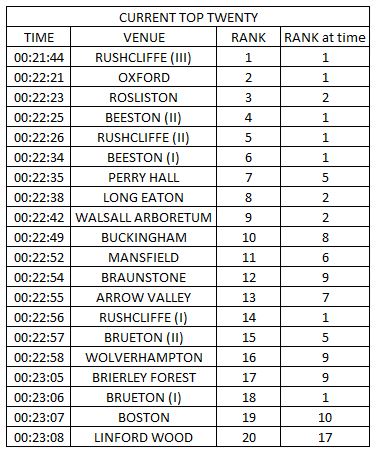
Every Saturday I join around 200,000 other runners and take part in a free 5k run at one of 1000 parks around the world (see http://www.parkrun.com). It's easy to keep statistics on how my times are improving. Alongside here is a table of my twenty fastest parkrun times.
I recorded those times at 16 different parks, and revisited some of them. As well as recording the rank of each parkrun time overall, I also record what its rank was when I ran that time, so for instance when I ran at Long Eaton, it was the second fastest I had run, but because some subsequent runs have been faster, it is now only my 8th fastest time.
Using the information in the table, can you work out in what order I ran the twenty parkruns?
A company orders in a variety of pieces of metal of lengths:
7cm 17cm 18cm 19cm 25cm 37cm 44cm
46cm 63cm 65cm 82cm 83cm 90cm 100cm
The quality controller, whose task it is to check the length of the incoming parts is correct, has figured out that he can use a straight rod of a particular length, and mark a series of points on it so that all of the lengths in the above list can be measured, either between two of the marks, or from an end to one of the marks. He uses the minimum possible number of marks.
How long is the rod, how many marks were made, and where were they positioned?

Fit a triangle, a rectangle, a pentagon and a hexagon into a circle of radius 10m.
What is the greatest combined area it is possible to achieve?
To celebrate the release of the Paddocks book: (click here), here is a brand new Paddocks puzzle you won’t even find in the book.

Draw fences between some of the posts so that each post is at the junction of exactly THREE fences.
These fences will divide the field into several PADDOCKS; any paddock whose area is greater than a single triangle will contain a NUMBER, which will indicate the area of the paddock, or in other words the number of TRIANGLES that make up the paddock.
The boundary fence is already in place, so any post on the boundary only needs one more fence emerging from it in order to make up its full complement.
For example:

Please visit and like my Facebook page: https://www.facebook.com/elliottlinepuzzles/
I’m proud to announce the publication of my third book: Paddocks!
http://www.lulu.com/shop/elliott-line/paddocks/paperback/product-23323543.html
I’m very proud of this book, it’s small but perfectly formed. Perfect for keeping it you pocket and taking out on long train journeys. Packed with over 100 hand-crafted puzzles, mostly Paddocks, but a smattering of other great puzzles to provide little breaks throughout the book.
To let you know the background, I came up Paddocks a few years ago, and it was very popular with the readers of my magazine, and later my website. It gained more traction when some of them were featured in Alex Bellos’ column in The Guardian, where it was very well received. Like Sudoku, they can be solved by pure deduction, and there is only one possible solution. Also like Sudoku, one deduction here might have a knock-on effect over there, as you gradually move towards the answer.
The task is to add fences within a field to divide it into Paddocks according to some very simple rules. It’s easy to learn, but difficult to master (the final puzzle in the book took me hours to test-solve!).
As it's print-on-demand the list price is quite high, but if you are a fan of Paddocks, or of logic puzzles in general, it’s well worth it. Amazon and other retailers take a big share, so the good news is if you go straight to lulu.com via the link above you get a massive 40% discount on the list price.
Thanks for your support!
Elliott Line
#supportindependentpublishing
I recently went on a bike ride where I noticed curiously that the start point, the finish point and the rest point were all exactly the same distance from my house.
The first leg of the ride involved riding 23 miles due east and then 7 miles due north, whereupon I arrived at the rest point.
The second leg of the ride involved riding 15 miles due east and then 9 miles due north to the finish.
How far is my house from the start/rest/finish points?
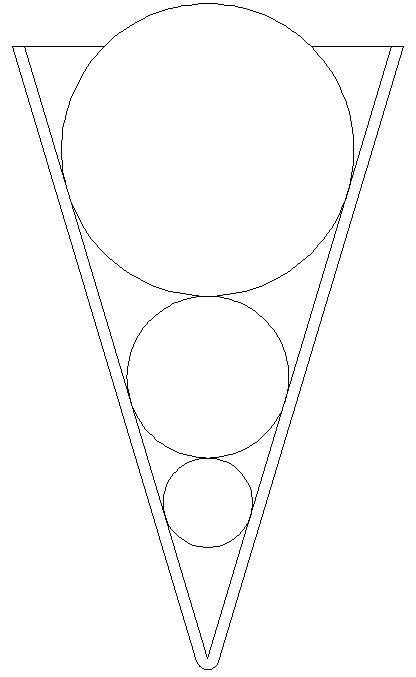
Three solid balls fit snugly into a conical container, so that each is just touching the inside of the cone all the way round, and just touching the ball above/below it.
The smallest ball, at the bottom of the stack, weighs 12kg. The largest ball weighs 147kg.
How much does the middle ball weigh?
Arrange these 15 ‘triples’ into 5 related words of 9 letters each:
ARM, CHA, COR, DER, EEK, FEN, IAN, ILE, INT, ISE, MOM, RAN, SPE, STA, UGR.
If you place a sphere inside a cube-shaped box that is only just big enough to contain the cube, the sphere will 52% fill the cube. The closest fraction to this, with a single digit numerator and denominator, is 1/2.
If you were to place 4 identical spheres inside a cube shaped box only just big enough to contain them, what proportion of the box filled by the spheres (to the closest single digit fraction)?
Three circular tables are placed against a wall, such that each table exactly touches the wall and the other two tables. The distance between the points where the two larger tables touch the wall is precisely 300cm. Given that the radius of each table is a whole number, how big are the tables?

Place the twelve 6-digit numbers into the grid (one digit in each cell), half of them left-to-right and half of them top-to-bottom.

What is the 6-digit number to be found along the main diagonal (from top-left to bottom-right)?
Draw a path that visits every dot once only. The path will be made only of horizontal and vertical lines. The path cannot cross itself or branch off, and must return to the start to form a complete circuit. Every third turning point in the circuit path has been marked by a triangle symbol.

It is well-known that a circle can be uniquely defined by three points on its circumference, providing they are not collinear.
I have ascertained that the analogous number of points needed to uniquely define an ellipse is five, with the condition that each of those five points lies strictly outside the quadrilateral formed by the other four.
What I don’t know is how, given the planar coordinates of the five points, you could discover other information about the ellipse, such as axis lengths, orientation and position. I’m not at all sure there is a method that will work in the general case.
In some specific cases, it is possible to work out the position, orientation and axes of the ellipse, given the co-ordinates of five points.
For instance, given the points (1,0), (2,0), (0,1), (0,2) and (1,2) lying on an ellipse, find the length of the minor axis.
Three people have to carry five boxes a distance of 120m from point A to point B. They each travel at a speed of 1m/s when carrying a box, or 2m/s when returning empty-handed for another box. Each person can carry only one box at a time.
What is the minimum time it will take them to carry all five boxes to point B?
People often ask where I get the ideas for my puzzles. This one has a typically mundane origin: I was bringing grocery shopping in from the car with my two children. There was more than we could manage in one trip so return trips were necessary. I started to wonder whether dropping groceries partway to the kitchen might be more efficient. We didn’t implement such a solution, but it did get me thinking about how I could reformulate the question as a puzzle, so here we are.