Below is a random array of 25 single digit numbers.
Somewhere in it are four numbers, whose positions within the grid form a square, and whose sum is also a square number. Can you find them?
Puzzle of the Week #56 - Ten Pin Bowling
The object of this game is to try to score as highly as possible by using letters in a given rack to form words. Just like in real ten pin bowling, you have a maximum of two attempts at each rack.
If you get a ten-letter word, that is a Strike and is worth 20 points.
If you find two words that between them use each of the ten pins once each, that is a Spare and is worth 15 points.
Any fewer than that, just total up the letters used to give your point total. So if you find a five-letter word and a three-letter word, that rack will have scored you 8 points.
What is the highest total you can achieve over the five racks?
Puzzle of the Week #55 - Alphasearch
Almost like a wordsearch, but instead of searching for words, you are searching for 3x3 arrays where the letters move strictly forward through the alphabet. Here are two possible examples:
There are five such arrays to find, can you find them all?
Puzzle of the Week #54 - Factorial over Square
Take the number 54! (the factorial of 54, the result of multiplying all of the positive whole numbers up to and including 54 - a number that is 72 digits long), and divide it by the largest square number that divides exactly into it.
The result is a number with 13 digits. What is it?
Puzzle of the Week #53 - Quotebreaker
I have taken a quotation, and I have replaced each of the letters with one-, two- of three-digit numbers according to the table below. Can you change it back to letters?
Be careful though, as some sequences of numbers could lead to several words, for instance 31110 could mean CAT (3,1,110), but could equally mean MAD (31,1,10).
This particular quotation is from the mathematician George Polya, and explains very succinctly why I enjoy puzzles.
1 13102111110 102110333311211102121 103333011211103 1 13102111110 100102332301131, 2111110 110201110211 21103 1 1310212132 3312 102110333311211102121 2132 1102011 1033330111110213332 3312 132121 100102332301131. 12133111102 100102332301131 311121 211 31331011103110, 2111110 2112 21110 3201303011321311103 12133111102 3111102213310321110121 13210 2102213213103 213211033 100301121 12133111102 213211211321102111211 1213111301102111103, 13210 2112 12133111 103333011211 21110 2121 12133111102 3311332 3111132103, 12133111 311121 1112010011102211132311 1102011 1101132103213332 13210 11322233121 1102011 110102211113110020 3312 102110333311211102121.
Puzzle of the Week #52 - Seven Towns
Norton lies 100 miles due north of Sutton.
Middleton is exactly halfway between Norton and Sutton.
Middleton is also halfway between Acton and Easton.
Barton is halfway between Acton and Middleton.
Weston is halfway between Barton and Norton.
Weston is due west of Easton.
The distance from Norton to Barton is the same as the distance between Acton and Sutton.
What is the distance from Weston to Easton?
Puzzle of the Week #51 - Pentominoes
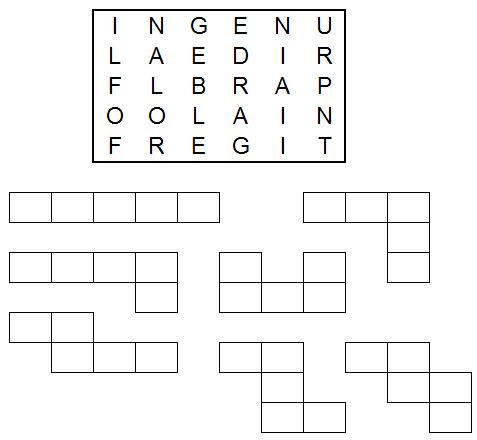
Divide up this grid of 30 letters into six five-letter words. Each word will be in the shape of a pentomino, specifically a pentomino that doesn't branch off or curl all the way around and contact itself.
The seven possible pentomino shapes are shown below the grid. Their reflections or rotations would also be possible shapes.
Puzzle of the Week #50 - Code
How could you decipher the following sentence?
iSpmyls aw pht eopisitnoo faehcp ia rfol teetsr ,ysbmlo sros apec.s
Puzzle of the Week #49 - Pair-of-Dice Regained
I have a pair of dice, which are numbered in an unconventional way. Unlike normal dice, where you can achieve a maximum total of 12, and often the same total can be achieved in several different ways, (eg 5+2=3+4=1+6=7, etc), these dice can total any number from 2 to 37 in exactly one way each.
All of the numbers on the dice are positive whole numbers, and one of the dice has four square numbers on it.
How are the dice numbered?
Puzzle of the Week #48 - The Wrong Vowels
Can you think of a common two-syllable English word, whose vowel sounds are a short 'o' and a short 'i', but which contains all of the vowels except 'o' and 'i'?
Puzzle of the Week #47 - Countdown Numbers
Using the numbers
1 2 3 4 5 6
at most once each, and using only the four standard mathematical operators, achieve the total of
532
Puzzle of the Week #46 - Pros and Cons
Below is a grid which you will need to fill with ten pairs of common words that differ only in that the first three letters of each word are ‘pro’ or ‘con’ (for example, ‘productivity’ and ‘conductivity’).
I have encoded all of the other letters as numbers.
Can you fill in the grid?
Puzzle of the Week #45 - Three Dice
I have three special dice. They are each 6-sided, and each has a positive whole number on each face.
Unlike standard dice, where the highest number achievable is 18, and many numbers can be achieved in several different ways, these special dice can total any whole number from 3 to 218.
The numbers on the first die total 174. The numbers on the second die total 348.
Level 1 challenge: what is the total of the numbers on the third die?
Level 2 challenge (for super-humans only): what numbers are on each of the dice?
Puzzle of the Week #44 - Step by Step
The answer to each of these clues is a five letter word. To get from each answer to the next, you replace one letter and then rearrange. For example if one answer was TRIAL, the next could be LATER. There is a link between the first and last answers.
League standings
Turning machine
Swindle
Arrive at
Preside over a meeting
Puzzle of the Week #43 - Hypothesis
You have in front of you five cards that are coloured on both sides. The five visible faces are red, blue, green, yellow and orange.
You are given a statement that:
‘If a card has red on one side it must have either blue or yellow on the other side’
You decide to turn over some of the cards in order to discover whether this statement is true or false. Which cards do you need to turn over?
Puzzle of the Week #42 - TriBall
TriBall is a sport which is played between two teams of three players.
My local TriBall club has an annual tournament.
In the tournament, every possible trio plays every other possible trio exactly once each. Luckily the ‘matches’ are only a couple of minutes in length, but even so the tournament takes a while to complete.
The club has one more member this year than it did last year. As a result, the total number of matches in the tournament is exactly three times as many as last year.
How many members are there in my TriBall club?
Puzzle of the Week #41 - Pascal's Wall
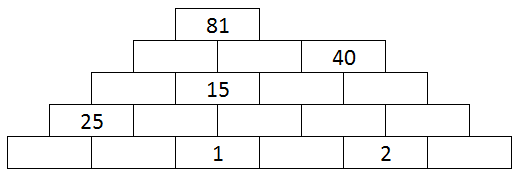
The number on each brick of Pascal’s Wall is the sum of the two numbers below it. Can you fill in all the blank bricks, and work out what the bottom row of bricks reads?
Puzzle of the Week #40 - Pyramid
And Lo! He did build a pyramid, and the base was a perfect square with area between one third and two thirds of an acre*. The length of each side of the square was an exact whole number of yards. The height of the pyramid was a prime number of yards, as was the distance from each corner to the apex.
What were the dimensions of the pyramid?
(* An acre is an area of 4840 square yards)
Puzzle of the Week #39 - Quotebreaker
I have taken a quotation, and I have replaced each of the letters with one-, two- of three-digit numbers according to the table below. Can you change it back to letters?
Be careful though, as some sequences of numbers could lead to several words, for instance 31110 could mean CAT (3,1,110), but could equally mean MAD (31,1,10).
31021111102111221110121 10211100102111031132110103 1 3121102131113033111103 33331213213 1103313111102011102 3312 1102011 11132213220212211101110 11321110213121 3312 1102011 320213010 1132111020 21110103 110010011021132110 33100100331032111011 13210 11321131121, 1102011 103113210311 3312 331021011102 2131100331031110 3332 1102011 10211033211003021321110 11011130110 213211011303021131132311.
Puzzle of the Week #38 - Palindromic Numbers
Some numbers are palindromic (reading the same backwards as forwards), such as 242, 12321 of 55.
38 is not a palindrome, or at least it isn’t when expressed in base 10.
However it is also a palindrome in three other bases (not including bases above base 38, where the number would be a single ‘digit’).
Can you find all three of them?
Some background on bases: we use base 10 all of the time, and we understand well how it works: each digit moving from right to left is worth 10 more than the last. Other bases work in exactly the same way, but with the digits increasing in value by a different factor. For example, 38 expressed in base 6 would be 102, since (62)x1 + (61)x0 + (60)x2 is equal to 38.