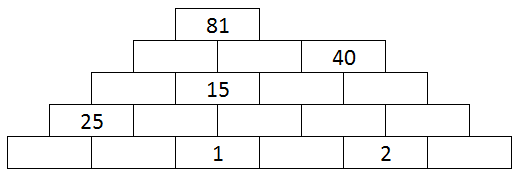
The number on each brick of Pascal’s Wall is the sum of the two numbers below it. Can you fill in all the blank bricks, and work out what the bottom row of bricks reads?
Puzzle of the Week #40 - Pyramid
And Lo! He did build a pyramid, and the base was a perfect square with area between one third and two thirds of an acre*. The length of each side of the square was an exact whole number of yards. The height of the pyramid was a prime number of yards, as was the distance from each corner to the apex.
What were the dimensions of the pyramid?
(* An acre is an area of 4840 square yards)
Puzzle of the Week #39 - Quotebreaker
I have taken a quotation, and I have replaced each of the letters with one-, two- of three-digit numbers according to the table below. Can you change it back to letters?
Be careful though, as some sequences of numbers could lead to several words, for instance 31110 could mean CAT (3,1,110), but could equally mean MAD (31,1,10).
31021111102111221110121 10211100102111031132110103 1 3121102131113033111103 33331213213 1103313111102011102 3312 1102011 11132213220212211101110 11321110213121 3312 1102011 320213010 1132111020 21110103 110010011021132110 33100100331032111011 13210 11321131121, 1102011 103113210311 3312 331021011102 2131100331031110 3332 1102011 10211033211003021321110 11011130110 213211011303021131132311.
Puzzle of the Week #38 - Palindromic Numbers
Some numbers are palindromic (reading the same backwards as forwards), such as 242, 12321 of 55.
38 is not a palindrome, or at least it isn’t when expressed in base 10.
However it is also a palindrome in three other bases (not including bases above base 38, where the number would be a single ‘digit’).
Can you find all three of them?
Some background on bases: we use base 10 all of the time, and we understand well how it works: each digit moving from right to left is worth 10 more than the last. Other bases work in exactly the same way, but with the digits increasing in value by a different factor. For example, 38 expressed in base 6 would be 102, since (62)x1 + (61)x0 + (60)x2 is equal to 38.
Puzzle of the Week #37 - Numbers Game
Using each of the numbers:
11 12 13 14 15 16
and only using basic arithmetic, it is possible to achieve the total of 987:
16 – 11 = 5
5 x 15 x 13 = 975
975 + 12 = 987
This method uses each of the numbers except for the 14.
There is a way to achieve the total of 987 by using all of the numbers once each. Can you find it?
Puzzle of the Week #36 - Double Elimination
To celebrate a new parkrun starting in Stratford-upon-Avon on Saturday, this week’s puzzle has a Shakespearean theme.
For each of the following, delete two letters from each word, and then re-space to give the name of a Shakespeare play.
For example CHARM LESS TEA = *HA*M LE** T** = HAMLET
1: JUMP LION UNSCARE SCARE
2: NASTY GHOUL SICK EDITS
3: JOKING CLEAN CAR
4: GIANT CORNY BRAN DISC LEMON PLAIT WRAP
5: TAP TIMID SOUR MIME EARNING THE TEAS DARED ARMY
6: HENCE GORY VIPER ARCTIC MINI
7: THE AIR FOILS MUST STAND CARESS ASIDE AIR
Puzzle of the Week #35 - Odd Word Out
What is the odd word in this list and why?
SEEK
BUY
TEACH
FIGHT
Notoriously, with odd-one-out questions, you will probably be able to find a reason why each of the words in turn should be the odd one. However, the true solution will be both convincing and satisfying, with even my choice of the odd word serving to support your hypothesis. Good luck!
Puzzle of the Week #34 – Euro Multiplication
I multiply a number which, when written in German, its letters are in alphabetical order, by a number which, when written in French, its letters are also in alphabetical order. The resulting product is a number which, when written in English, its letters are in alphabetical order.
What are the numbers?
Puzzle of the Week #33 - Cryptic Quiz
I am a fan of the BBC Radio 4 show Round Britain Quiz. I have written a question in the style of the show:
Delve beneath the surface and you’ll find the following several leagues below:
300 sprightly sounding Greeks
The Blue Boy, his father and a ghost
Urban arboreal grey matter
And a handcart
What are they?
Puzzle of the Week #32 - Streetlife
Fifteen friends are dotted around a city. They wish to meet up. They can only travel along streets and avenues.
Where should they meet that would minimise the total distance travelled?
Puzzle of the Week #31 - Engine Failure
This is an excerpt from my first book, Very Clever Puzzle Compendium: http://www.lulu.com/spotlight/maxelkat
Orville and Wilbur are model aeroplane enthusiasts.
Orville: These new engines you bought are terrible – they keep breaking down in mid air.
Wilbur: I know! That’s why I’ve fitted my new plane with two engines, and as long as at least one of them is still working, it will continue to fly.
Orville: I’ve gone even better: I’ve fitted mine with four engines, and as long as at least two of them are still working, my plane will stay up.
Wilbur: That’s not necessarily better – it depends on exactly what the probability is of each of the engines failing.
Orville: How do you mean?
Wilbur: Well, for instance, if the individual engines break a quarter of the time, the chance of your plane falling from the sky just over five percent, and mine would fail just over six percent of the time.
Orville: So mine would be better!
Wilbur: Yes, but what if the engines break down exactly half of the time? My plane would come down a quarter of the time, and yours would crash just over thirty-one percent of the time – so mine would be better!
As it turned out the probability of each of the engines malfunctioning was a magic figure somewhere between one quarter and one half, where the probability of Wilbur’s two-engine plane and the probability of Orville’s four-engine plane crashing was exactly identical.
What was the probability of each engine failing?
Puzzle of the Week #30 - Shadowbox
This is an excerpt from my second book, Shadowbox Logical Crossword Puzzles: http://www.lulu.com/spotlight/maxelkat
Place all of the words into the grid, crossword style.
A grey square will either contain a vowel (A, E, I, O, U) or will become a black square.
A white square will contain a consonant.
The final arrangement of black squares and letter squares will be symmetrical in horizontal, vertical and diagonal directions.
Puzzle of the Week #29 - Non-Alcoholic
Can you name a non-alcoholic drink which has mead in it?
Puzzle of the Week #28 - Vase (part 2)
This puzzle re-uses the same glass vase from Puzzle of the Week #26. I added an encoded solution in the comments of that question.
I have a glass vase, with a square base and vertical sides. The vase is 50mm x 50mm, and 260mm high. The bottom 10mm is solid glass, and the remaining 250mm has 1mm thick glass walls.
The density of glass is 2.4 times that of water. When I pour a small amount of water into the vase, the centre of gravity is brought down slightly. As more water is added, at a certain point the centre of gravity will begin to creep back up.
How much water added to the vase, to the closest millilitre, will give the lowest centre of gravity for the vase and its contents?
Puzzle of the Week #27 - Dice Logic
Four cube-shaped dice have a different letter on each of their faces, so that between them they feature the first 24 letters of the alphabet, A to X, exactly once each.
I throw the four dice, and make a note of the four uppermost faces. I do this repeatedly, the results of which are shown below. Can you work out what letters are on each of the dice? The letters on one of the dice can be rearranged to form the surname of some famous brothers.
ACDI BKNW BHMO CNSW CIPQ CHSU CGLN DFRU DEOR DHVX EIMU FNST FILO JMNW QTUV
Puzzle of the Week #26 – Vase (Part 1)
I have a glass vase, with a square base and vertical sides. The vase is 50mm x 50mm, and 260mm high. The bottom 10mm is solid glass, and the remaining 250mm has 1mm thick glass walls.
To the nearest millimetre, how high is the centre of gravity (from the base of the vase)?
Puzzle of the Week #25 - Transportation to Occupation
Can you take a nine letter word for a type of large ship, and insert two new letters (without changing the order of the original nine letters) to form an eleven letter word for a heroic job?
Puzzle of the Week #24 - parkrun Vowels
This week's puzzle lies at the intersection of two of my interests: puzzles and parkrun.
There are currently 374 senior UK parkrun venues; these can be found at www.parkrun.org.uk/events
There are three events whose names contain all five vowels (a, e, i, o, u). Can you find them?
Puzzle of the Week #23 - SE Words
Can you think of five four-letter words, each beginning with SE?
Sounds simple, however you cannot use a letter more than once, and you can’t re-use the S or the E anywhere else. So for instance, SELL is not allowed, as it has two Ls, SEEK is not allowed as it repeats the E, and you cannot have both SENT and SEAT, as both have a T, but either word is acceptable on its own.
Puzzle of the Week #22 - Hex-Agony
I have a hexagon, with six sides of equal length. Opposite pairs of sides are parallel, and the distances between these parallel sides are 7cm, 8cm and 9cm respectively.
What is the area of my hexagon?