Your Custom Text Here
If we call the radius ‘r’ and the height from the centre of the circle to the diagonal line ‘a’, then by Pythagoras we have:
49^2 = r^2 + a^2
Using intersecting chords theorem, 49*31 = (r+a)(r-a)
49*31 = r^2 – a^2
If we take the first equation and subtract the second we get:
49(49-31) = 2a^2
a^2 = 49*9
a = 21
The height of the triangle is twice this distance ‘a’, and is therefore 42.
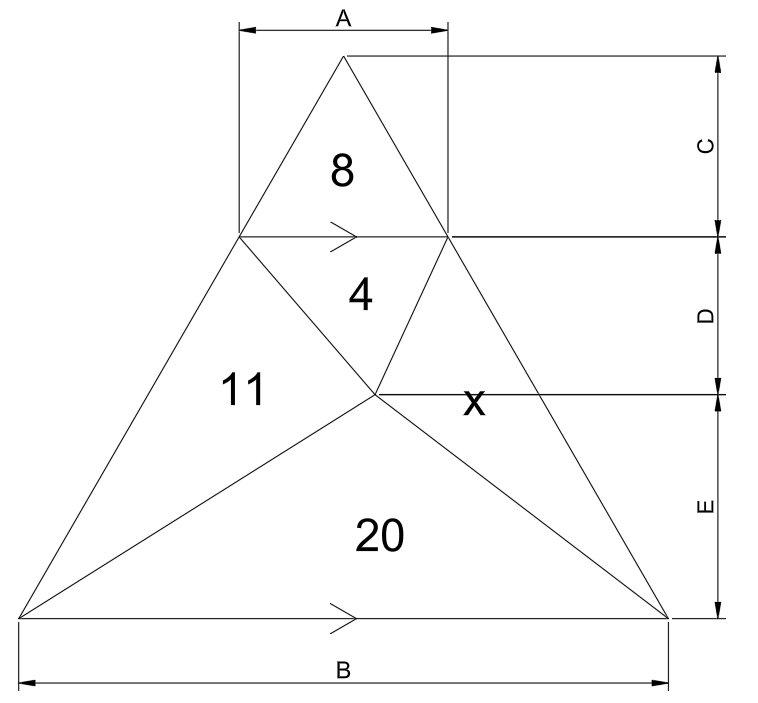
The area of the third region is 4.
I’m going to show that this is the case a little back-to-front, by presupposing that the overall area of the nonagon is 9, and then proving that that is in fact the case.
First of all I hope it’s evident that there is exactly one size of nonagon for which, if you form a triangle of area 2 using one side as the base and a vertex somewhere opposite, that the region to the left has area 3. That being the case, if we find a size of nonagon that works, that is THE solution.
So next I’m going to claim that the overall area is 9 (and therefore the missing are is 4) and show that that does indeed work.
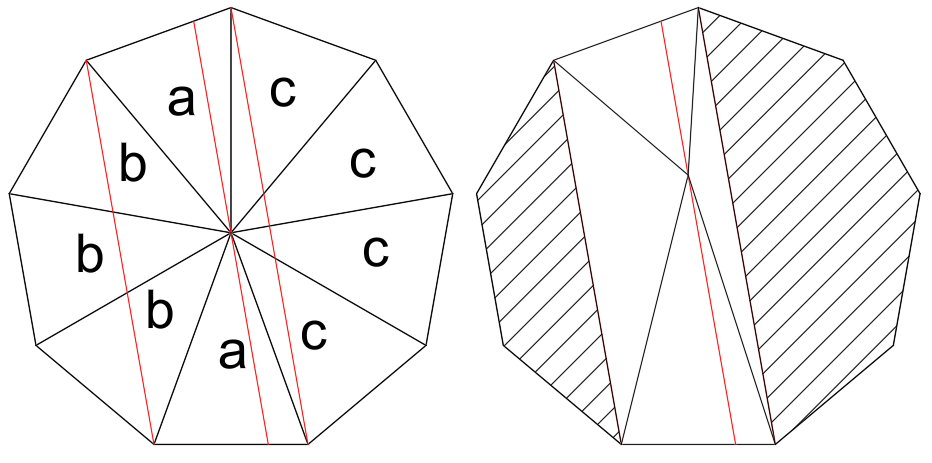
Drawing lines from each of the vertices to a point in the exact centre will divide the nonagon into 9 equal regions of area 1, therefore the combined area of the a regions is 2, of the b regions is 3, and of the c regions is 4.
The red lines are all parallel – the left and right ones are parallel because of the inherent symmetry of a regular nonagon, and I have defined the middle red line to be parallel to the others and passing through the centre of the nonagon.
In the second figure we can see that if we moved the point that all of the vertices of the nonagon were connected to (the hub if you will), but ensured it stayed on this middle red line, that the combined area of the b regions would remain 3. This is because the left shaded region is unaffected by the change, and the other part of the b region is a triangle with a fixed base and a fixed altitude.
The exact same rationale applies to the c region, which will remain 4 regardless of where on the middle red line the hub is.
Finally the a region will remain area 2, because the overall area of 9 is unaffected, and the a region includes everything not in either the b or c regions. This being the case we can let the hub move all the way to the top edge of the nonagon, meaning that the a region becomes a single triangle, and the b and c regions remain 3 and 4 respectively.
For the person to have their 50th birthday on the same weekday as they were born, they will have to have been alive through 13 leap days. (50 extra days, one for each year, plus 13 leap days = 63: 9 weeks).
Ordinarily this will happen if they were born in the two year period immediately preceding a leap day. If they were born in the two year period immediately after a leap day they will only have lived through 12 leap days. However the situation is complicated by the fact that century years are only leap years if the number of the century is divisible by 4, so 1700, 1800 and 1900 were not leap years. So for people born in the latter half of the 1600s, 1700s or 1800s, it’s impossible to live through 13 leap days in their first 50 years. This means that the probability of the person celebrating their 50th birthday on the same weekday as they were born is roughly 5/16.
This deals with every case except for if the person was born on the 29th of February, which is difficult to account for as it is unclear exactly when they would celebrate their birthday in a non-leap year (which their 50th would certainly be).
The only solution is: (2+1/3)(2+1/5)(2+1/7) = 11 (or some ordering of a,b,c = 3,5,7).
7/3 * 11/5 * 15/7 = 11
(2+1/a)(2+1/b)(2+1/c) = d
((2a+1)/a)((2b+1)/b)((2c+1)/c) = d
(2a+1)(2b+1)(2c+1) = abcd
All of the three terms on the left are odd, so a b c and d must all be odd primes.
Each term (2+1/p) must therefore be between 2 and 2 1/3, and so d must be between 8 and 12.7, and there is only one prime number in that range: 11, so d=11
One of the (2p+1) terms must be a multiple of 11. Without loss of generality we can say it is (2a+1). a must therefore be of the form 5+11n. 5 is prime, so let’s explore that possibility:
Let’s say that a is 5 and d is 11.
This leaves (2b+1)(2c+1)=5bc. Let’s say (2b+1) is divisible by 5.
b must be of the form 2+5n. 2 is prime, however we know we are looking for an odd prime. Let’s try 7. That leaves:
15(2c+1)=35c
30c+15=35c
5c=15
c=3, which is prime, so everything works.
I’ll leave it to the reader to satisfy themselves that this is the only solution.
ab + c = 12
bc + a = 12
ca + b = 12
The fact that we are told there are five answers is a clue as to what they might look like. If there was a solution with a b and c all distinct, that would form 6 answers alone, so can’t be possible. If there is a solution where two of the numbers are equal and the third is different, that would account for three answers. Assuming that is the case the remaining two answers must be when all three values are the same.
The solutions are that either two of the numbers are 1 and the other is 11 (this accounts for three of the five answers), or all three are 3, or all three are -4.
If you divide each brick into four as shown, each of those quarters will have the same proportions as the original brick. We can say without losing generality, that the height of each of these new bricks is 1. If we call the length of each of the mini bricks ‘x’, this value will be the proportion we are seeking.
If we make a Pythagorean triangle in two different ways as shown, their hypotenuses will both be equal to the circle radius R.
R^2 = (2x)^2+3^2 = (3x)^2 + 1^2
4x^2+9 = 9x^2+1
5x^2 = 8
x^2 = 8/5
x = sqrt(8/5) = ~1.265
so the proportion of each brick’s length to its height is ~1.265
The circle has an area of 4225*pi, which is approximately 13273m^2.
If we draw an inscribed dodecagon in each circle, then a necessary condition for the area being rational is that the number of convex borders is cancelled out by the number of concave borders. This is only the case for region C.
Region C has an area of exactly 1. You can verify this by tessellating the shape and overlaying a unit square:
Incidentally every area can be written as x*pi + y*sqrt(3) + z, where x, y and z are rational numbers. I had fun working them all out.
Asking for the probability was a deliberate red herring, since it’s actually impossible for the last pebble to be white.
The only way of removing black pebbles is if both selected pebbles are black, at which point they are both discarded. But since we start with an odd number of black pebbles, we will still have an odd number of black pebbles throughout the game. Therefore the final pebble will be black. The probability the last pebble is white is 0.
If we scale up the figure by the square of the hypotenuse of the 5,12,13 triangles, (namely 169), then the fourth triangle will have sides of 828,2035,2197 and since these numbers have a GCD of 1, that is the primitive form of the Pythagorean triangle we were seeking.
There are two possible arrangements where all the lengths are integers, but in both the red line is 2304 long.
The height is at a minimum when the four triangles are similar, and so therefore the bottom right corner will be four equal angles of 22.5 degrees. The length of the first hypotenuse will be sec(22.5), and the second will be the square of that, etc. The height of the rectangle will be the fourth power of sec(22.5) which is equal to 24-16*sqrt(2), which is approximately equal to 1.3726.
We are given:
1/a = 1+b
1/b = 3+c
1/c = 4+b
If we invert the third equation we have an expression for c that we can use in the second equation.
c=1/(4+b)
1/b = 3+1/(4+b)
1/b = (3(4+b)+1)/(4+b) = (13+3b)/(4+b)
Cross multiplying we get a quadratic:
3b^2+12b-4 = 0
The value of b that lies between 0 and 1 is (4*sqrt(3)-6)/3
We can put this into the first equation:
1/a = 1+(4*sqrt(3)-6)/3 = (3+4*sqrt(3)-6)/3 = (4*sqrt(3)-3)/3
a = 3/(4*sqrt(3)-3), which does fulfil the requirements of the question, but we’d prefer to not have irrationals in the square root:
a = 3/(4*sqrt(3)-3)*(4*sqrt(3)+3)/(4*sqrt(3)+3)=
(12*sqrt(3)+9)/(48-9) = (4*sqrt(3)+3)/13
Since, if we find a valid figure we can scale it by ‘h’ in the horizontal and ‘1/h’ in the vertical to find any one of an infinite family of solutions, we can, without loss of generality, specify the particular figure where A = C. And since that top triangle of area 8 is similar to the figure as a whole we can also say that B = C+D+E.
A and C must both be equal to 4 to form the triangle of area 8. To form the triangle of area 4, D must equal 2.
From the triangle of area 20, B*E must be 40.
We know that B = C+D+E, and we also know the values of C and D, therefore E = B-6. So B*(B-6)=40. We could solve this as a quadratic, or else we can just look for two positive numbers 6 apart whose product is 40, namely 10 and 4.
So if B = 10, the entire figure has area 50, and if we subtract the known areas we find that area x = 7.
PS: If I wanted to be a little more general I would just multiply all of the horizontal lengths in the above solution by h and all the vertical distances by 1/h and when calculating the areas all hs would cancel.
I’m going to make use of a theorem called Ceva’s Sine theorem, which states that, in the below figure, the product of the sines of angles a, c and e is equal to the product of the sines of angles b, d and f.
In our question, a and d are unknown, and b, c, e and f are 6, 24, 12 and 54 respectively.
sin(a).sin(24).sin(12) = sin(6).sin(d).sin(54)
(sin(24).sin(12))/( sin(6).sin(54)) = sin(d)/sin(a)
sin(d)/sin(a) = 1
sin(d) = sin(a)
But since the six angles must total 180 degrees, a + d = 84, therefore a = d = 42.
So our unknown angle x is equal to 42 degrees.
The merged lane will need to have twice as many cars passing a given point in a given time period than the initial pair of lanes, or conversely will take half the time for each car to pass a given point.
Say the initial speed is x (mph), then the stopping distance is (x^2)/20 + x/2 (ft).
If we take this distance and divide by the speed x we will know the time taken for each car to pass a given point. (The units for this are 15/22 seconds, but we don’t need to worry about that since it’s the same whatever the speed).
The formula for this measure is x/20 + 1/2.
To merge the lanes we need to find a value y such that y/20 + 1/2 is half as much as x/20 + 1/2:
y/10 + 1 = x/20 + 1/2
y/10 = x/20 – 1/2
y = x/2 – 5
For our puzzle x=60, and so therefore y = 25mph.
The maximum is 81643572, 27+16+7+12=62
The minimum is 27163548, 9+4+7+8=28
Since both 8 and 4 are powers of 2, we can rewrite them as 2^3 and 2^2 respectively:
2^(3(x-1)) = 2^(2(x+2))
2^(3x-3) = 2^(2x+4)
3x-3 = 2x+4
x = 7
3x-3 = 2x+4 = 18
2^18 = 262144
N is equal to 262144.
It turns out that the largest semicircle, the one with unit radius, sits in the middle of the segment.
The circle radius is 2, and the segment has an angle to the centre of the circle of 120 degrees.
You might notice that each pair of adjacent terms has a GCD greater than 1, for instance 21 and 119 are both divisible by 7, and 697 and 4059 are both divisible by 41. In fact on further inspection, each term appears to be the product of adjacent terms of a second sequence: 1,3,7,17,41,99,etc. It looks as if the definition of this second sequence (after the initial two terms) is that each term is twice the previous term, plus the term before that. If that is confirmed to be the case, the only way a term in the product sequence can be prime is if one of the two factors is 1 (and the other is itself prime). This is only the case for the term ‘3’, and so therefore this is the only prime number that will appear in the entire infinite sequence.
But how do we prove that the given sequence is the products of adjacent terms of the second sequence?
That is equivalent to proving the claim that if a=2b+c, b=2c+d and c=2d+e then it follows that ab=5bc+5cd-de.
Let’s start with the product relation but substitute a=2b+c
(2b+c)b=5bc+5cd-de
2bb+bc=5bc+5cd-de
2bb=4bc+5cd-de
Next replace any instances of b with 2c+d
2(2c+d)(2c+d)=4(2c+d)c+5cd-de
8cc+8cd+2dd=8cc+4cd+5cd-de
2dd=cd-de
Finally replace c with 2d+e
2dd=(2d+e)d-de
2dd=2dd+de-de
Since both sides are evidently equal, that proves that the three relations are equivalent to the product relation.