Puzzle of the Week #268 - Dice Game

This puzzle is based on a dice game my son and I invented, involving 12-sided, 10-sided, 8-sided and 6-sided dice. (As with modern convention I will be using the word ‘dice’ to refer to both the plural and the singular, rather than the more archaic ‘die’).

In round 1, both players each have a 12-sided dice. They roll them and the player with the lowest number loses that round (if the numbers are equal they both simply roll again). The losing player exchanges their 12-sided dice for a 10-sided dice for the second round.

The game continues such that at each round the loser changes their dice for one with two fewer sides. The final round occurs when one of the players has to roll a 6-sided dice. The winner of this round is the overall winner of the game (even if they lost all of the previous rounds).

Since the game is symmetrical, the probability of each of the players winning is 50%, but the puzzle question is, how important is the first round? What is the probability that you win the overall game if you win/lose the initial round?

Puzzle of the Week #267 - Tetrahedron Game

In this game there is a grid of 22 triangles, four of which are painted. You may initially place a tetrahedron on any triangle you want but from there forward you move by ‘rolling’ the tetrahedron over one of its edges so that it will then be on an adjacent triangle on the grid and resting on a different face of the tetrahedron. If you roll onto a painted triangle, the paint transfers to that face of the tetrahedron (unless that face is already painted), and when a painted face of the tetrahedron lands on an unpainted triangle, the paint is transferred from the tetrahedron to the triangular grid.

The object of the game is to continue to roll around the grid until all four faces of the tetrahedron are painted, however only one of the four grids shown can actually be solved. The other three are not solvable regardless of where the tetrahedron is initially placed.

Which is one that can be solved?

tetrahedron puzzle.JPG

Puzzle of the Week #266 - Base Four Code

I have taken a quotation, and I have replaced each of the letters with the numbers that denote their position in the alphabet. However, I have used the base 4 number system. 

base4.JPG

Be careful, as some sequences of numbers could lead to several words, for instance 31110 could mean CAT (3,1,110), but could equally mean MAD (31,1,10). 

132121333211  1132033  10311033100103  3011110232213213  21103  333010,  11320111102011102 1101131132110121  33102  11211320110121.  132121333211  1132033  231111100103  3011110232213213 1031101121103  121331113213.  1102011  1310211111011103110  11020213213  12133111  3132  1033  21103 231111100  12133111102  31213210  121331113213.

Puzzle of the Week #261 - Su-Dot-U

Your task is to solve this irregular sudoku (the digits 1 to 5 appearing once each in every row, column and 'shape').
Except that I haven't told you where the boundaries between the shapes are; instead I've placed dots in any square where the number to be placed in the square denotes how many squares (including the one with the dot in) until you get to the next boundary line in the direction of the dot.
Clear as mud? Hopefully the attached example 3x3 will help. For instance, the 2 in the middle of the top row, combined with the left and right dots, says that in each direction left and right from that square there are two squares (including the one with the 2 and the dots in) before you get to a boundary line (which happens to be the outer boundary of the entire grid).
In both the example and the puzzle, I have placed dots in every position that I could, according to the rules.

A hint to get you started: if a dot appears next to the outside boundary of the grid, then that square must contain a 1.

sudotu3.JPG

Puzzle of the Week #260 - Semi-grams

Rearrange the letters in each of these ten five-letter words and then pair them up to form five ten-letter words. I’ve completed one of the ten letter words to start you off:

First halves:

(ALERT)    METRO    NOTED TIMES    UPSET

Second halves:

GIANT    (RATIO)    ROAST SENSE    SOUND

Example solution:

ALERT + RATIO = RETAL + IATOR = RETALIATOR

Puzzle of the Week #258 - Su-Dot-U

Back by popular demand!

Your task is to solve this irregular sudoku (the digits 1 to 6 appearing once each in every row, column and 'shape').

Except that I haven't told you where the boundaries between the shapes are; instead I've placed dots in any square where the number to be placed in the square denotes how many squares (including the one with the dot in) until you get to the next boundary line in the direction of the dot.

Clear as mud? Hopefully the attached example 3x3 will help. For instance, the 2 in the middle of the top row, combined with the left and right dots, says that in each direction left and right from that square there are two squares (including the one with the 2 and the dots in) before you get to a boundary line (which happens to be the outer boundary of the entire grid).

In both the example and the puzzle, I have placed dots in every position that I could, according to the rules.

A hint to get you started: if a dot appears next to the outside boundary of the grid, then that square must contain a 1.

sudotu 2.JPG

Puzzle of the Week #256 - Su-Dot-U

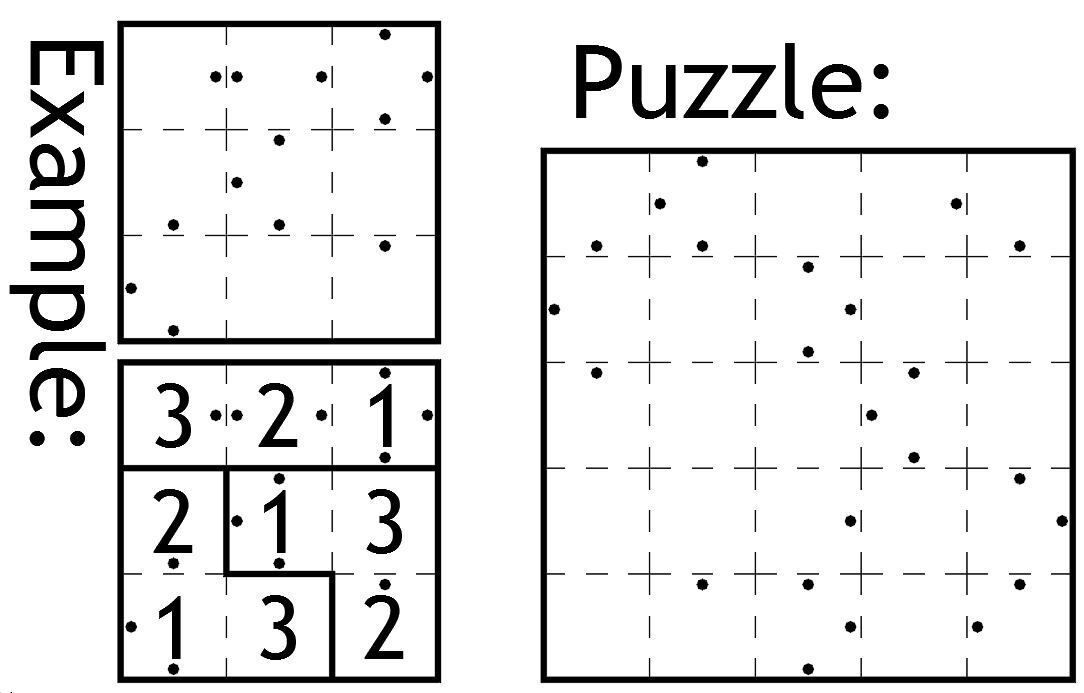
Your task is to solve this irregular sudoku (the digits 1 to 5 appearing once each in every row, column and 'shape').
Except that I haven't told you where the boundaries between the shapes are; instead I've placed dots in any square where the number to be placed in the square denotes how many squares (including the one with the dot in) until you get to the next boundary line in the direction of the dot.
Clear as mud? Hopefully the attached example 3x3 will help. For instance, the 2 in the middle of the top row, combined with the left and right dots, says that in each direction left and right from that square there are two squares (including the one with the 2 and the dots in) before you get to a boundary line (which happens to be the outer boundary of the entire grid).
In both the example and the puzzle, I have placed dots in every position that I could, according to the rules.

A hint to get you started: if a dot appears next to the outside boundary of the grid, then that square must contain a 1.

su-dot-u.JPG

Puzzle of the Week #253 - Build-a-Crossword

I have taken a completed crossword grid, removed all the consonants to the end of the row and/or column that they belong in, and then changed all the black squares into random vowels.

Your task is to reconstruct the crossword by figuring out which of the vowels are genuine and which need to become black squares, and by putting the consonants all back into place. Good luck!

BUILDACROSSWORD PUZ.JPG