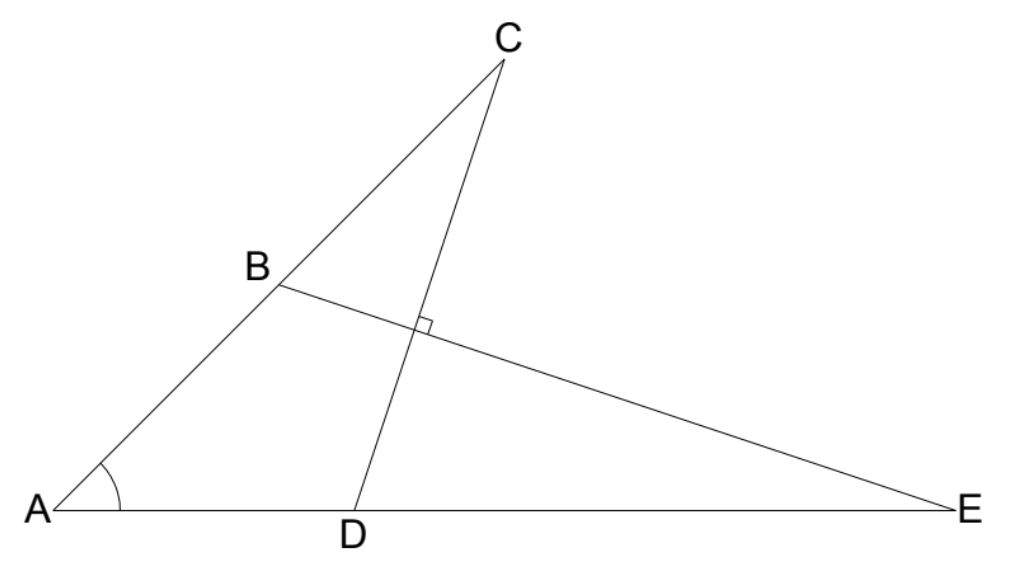
B is the midpoint of AC
D is one third of the way along AE
CD is perpendicular to BE
AE is (√2) times the length of AC
What is the angle at A?
Your Custom Text Here
B is the midpoint of AC
D is one third of the way along AE
CD is perpendicular to BE
AE is (√2) times the length of AC
What is the angle at A?
The towns of Abbottsville, Beresford and Christchurch all lie on one straight road. I embark on a journey from Abbottsville, through Beresford, to Christchurch, and back the same way. Each day I cover 1 mile more than the day before. It takes me 10 days to travel from Abbottsville to Beresford, 11 days to travel from Beresford to Christchurch and 12 days to travel from Christchurch (through Beresford) to Abbottsville.
What are the distances between the towns?
The open beta has now started 🎉
Also, there’s now a little trailer on the store page (link to the trailer: https://www.youtube.com/watch?v=is8n293Z_zs).
Unfortunately, Google doesn’t offer Instant Apps for beta versions, so at the moment there is no free
demo available. We can hopefully get that sorted in the next few days.
Moritz Neikes has done a tremendous job with the app, thank you Moritz!
Which of the following scenarios should on average* take the most throws:
Repeatedly tossing a coin until you have seen at least 6 heads and at least 6 tails, or
Repeatedly throwing a dice until you have seen each of the numbers 1 to 6 at least once each?
*(simple arithmetic mean)
Find a set of three (different positive whole) numbers whose sum is 6! And whose product is 9!
Find a set of four different positive whole numbers whose sum is a factorial number and whose product is also a factorial number.

A glass tumbler has an outside diameter of 78mm, and inside diameter of 72mm and a solid base that is 30mm deep.
Its centre of gravity is exactly 30mm from the table, ie, at the height of the bottom of the inside of the glass.
What is the overall height of the glass tumbler?
I have a sequence. It begins:
1
101
10101
1010101
101010101
etc
As it’s populated entirely with 1s and 0s it is not entirely clear whether these are decimal numbers, or binary numbers, or some other base entirely.
Construct a formula to give the nth term, which works no matter what base we are working in.
***EDIT*** You are looking for a simple formula where you plug in the value of n and get the nth term, no recursive formulae or finite sums required.
I’ve taken the name of a particular sub-national region of a large country and split it apart. It is possible to use each of the following as a filling in the ‘sandwich’ to create three words:
_____R_____
_____CH_____
_____INL_____
What is the name of the region?
1/3 = 0.333… and 3/8 = 0.375. No fraction with a single-digit denominator lies between them.
What is the fraction greater than 1/3 and less than 3/8 that has the lowest denominator? Call that fraction ‘x’.
What is the fraction greater than ‘x’ and less than 3/8 that has the lowest denominator? Call that fraction ‘y’.
Finally, what is the fraction greater than ‘x’ and less than ‘y’ that has the lowest denominator?
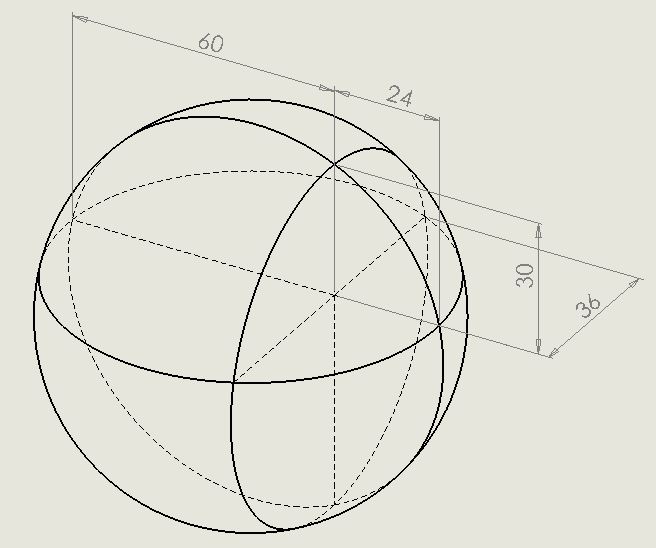
A perfectly spherical asteroid is in orbit somewhere in the solar system. There is a small deposit of Unobtainium buried within it.
Scientists are able to scan the asteroid and determine the position of the deposit of Unobtainium relative to the surface of the sphere, by imposing a perpendicular coordinate system on it:
From the Unobtainium, if you go the 24 metres in the positive x direction you reach the surface
From the Unobtainium, if you go the 60 metres in the negative x direction you reach the surface
From the Unobtainium, if you go the 30 metres in the positive y direction you reach the surface
From the Unobtainium, if you go the 36 metres in the positive z direction you reach the surface
What is the radius of the spherical asteroid?
This may help you: The general equation of a sphere is: (x - a)² + (y - b)² + (z - c)² = r², where (a, b, c) represents the centre of the sphere, r represents the radius, and x, y, and z are the coordinates of the points on the surface of the sphere.
I recently investigated which numbers can be represented at the sum of one square number and double a different square number, for instance 9 is 1+2(4), or 38 is 36+2(1).
With pencil and paper: 99 is the smallest number that can be represented as a^2 + 2b^2 in three different ways: find them all!
With a computer: what is the smallest number that can be represented as a^2 + 2b^2 (with a and b different positive integers) in six different ways?

I have a number.
I multiply each of the digits together to get another number.
I multiply each of the digits of that number together, and I find that I get the number 36.
If you disallow the use of the digit 1 (for obvious reasons) there are only two numbers I could have started with, what are they?
Which is greater:
the 789th number in the 123 times table to begin with the digits 456,
or the 123rd number in the 789 times table to begin with the digits 456?

An expedition is being planned to climb a truncated conical volcano that is 40km diameter at the base, and 24km diameter at the crater edge. The slope length is 12km.
The path starts at A at the base and ends at point B on the crater edge, exactly halfway round the volcano from A.
What is the length of the shortest possible route around the conical face of the volcano (to the nearest km)?
Bakewell parkrun is a picturesque free, weekly, timed 5km run along the Monsal trail in Derbyshire. The course heads off 2.5km along the trail, then takes a u-turn, before heading back to the start/finish.
Two friends run the parkrun, both starting at the same time (Saturday 9am). They run at different paces, but their paces are consistent. Nicola, the faster of the two, reaches the turnaround point first, then exactly two minutes and twenty seconds later, passes Danny travelling the other way. At the finish, Nicola has exactly twelve minutes to wait before Danny crosses the finish line.
How long do Nicola and Danny take to complete their parkruns?
Runners will know, if they want to predict what time they should be aiming for in, say, a 10km race, based on what they can do at 5km, you should do more than merely doubling the time: the longer a race, generally the slower you need to go. One useful rule is known as the 6% rule. It isn’t unfortunately as simple as merely doubling the 5km time and adding 6% - instead it is raising the ratio of distances to a power of 1.06.
So (10/5)^1.06, would give you a factor of around 2.085. Multiply this by your typical 5km time and you should be looking at that for your 10km time.
Of course, this is only a rule of thumb, so will be more true for some people than for others. For one athlete, let’s call him Norm, he finds that his personal best times, at a variety of distances, precisely follow the rule (to the nearest second). His half-marathon best time is exactly 1 hour more than his 10km best time. (A half-marathon in metres is 21097.5).
What are his 10km and half-marathon personal bests?
This conversation took place on a particular day of the (non-leap) year:
“Isn’t it curious,” remarked Izzie, “that if you take today’s date, double the date number and double the month number, you get my birthday?”
“Interesting!” replied Leila, “but if you consider today as the ‘n’th day of the year and work out what the ‘2n’th day of the year is, you get MY birthday!”
Izzie’s and Leila’s birthdays are in the same calendar month.
When did this conversation take place and when are the girls’ birthdays?
Can you add two more bars to this digital display to make it a multiple of 13 that is NOT 78?
