Puzzle of the Week #23 - SE Words

Can you think of five four-letter words, each beginning with SE?

Sounds simple, however you cannot use a letter more than once, and you can’t re-use the S or the E anywhere else. So for instance, SELL is not allowed, as it has two Ls, SEEK is not allowed as it repeats the E, and you cannot have both SENT and SEAT, as both have a T, but either word is acceptable on its own.


Puzzle of the Week #18 - Egyptian Fractions

In ancient Egypt, they only liked to use so-called unit fractions, which are fractions that have 1 as the numerator. If they wanted to represent a fraction that wasn't already a unit fraction, they would express as the sum of different unit fractions.

So, for instance 3/4 = 1/2 + 1/4. and 2/7 = 1/4 + 1/28.

How can you express 39/50 as a sum of different unit fractions?

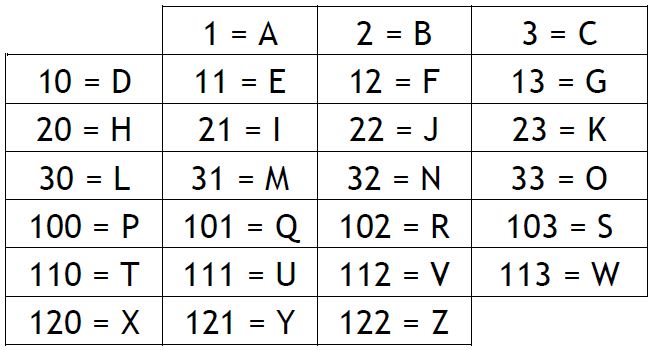
Puzzle of the Week #17 - Quotebreaker

Quotebreaker is back by popular demand! I have taken a quotation, and I have replaced each of the letters with one-, two- of three-digit numbers according to the table below. Can you change it back to letters?

Be careful though, as some sequences of numbers could lead to several words, for instance 31110 could mean CAT (3,1,110), but could equally mean MAD (31,1,10).

213210313211 10011331003011 110211 1301131121103 10311110211 110201110 1102011121 110211 12213211. 21110 21103 333230121 1102011 10313211 10011331003011 1132033 110211 113213030213213 11033 1103121110 110201110 1102011121 110211 31021122121.


Puzzle of the Week #15 - Bolt Head

I’ve used a micrometer to measure a bolt head, both from edge to edge, and from point to point.

I later realise that I had forgotten to ‘zero’ the micrometer before I used it, meaning that both measurements are wrong, but they are wrong by the same amount.

What should the measurements be?

Puzzle of the Week #14 - NE Words

Can you think of five four-letter words, each beginning with NE?

Sounds simple, however you cannot use a letter more than once, and you can’t re-use the N or the E anywhere else. So for instance, NELL is not allowed, as it has two Ls, NEON is not allowed as it repeats the N, and you cannot have both NETS and NEAT, as both have a T, but either word is acceptable on its own.

Puzzle of the Week #13 - Sloping Wall

I've built a sloping wall, on level ground. One end is 10ft high, and the other end is 15ft high.

I attach a piece of string from each top corner to the opposite bottom corner, forming an 'X' shape. Assuming the strings are pulled tight, what height from the floor is the point where the two string cross?

Puzzle of the Week #9 - Third Avenue

Draw a path that visits every dot once only.

The path can be made only of horizontal and vertical lines.

The path cannot cross itself or branch off, and must return to the start to form a complete circuit.

Every third turning point of the path has been marked with a triangle symbol. In other words, at each symbol there will be a 90 degree turn in the path, and there will be two further 90 degree turns before the next symbol.

​


Puzzle of the Week #8 - Quotebreaker

Quotebreaker is back by popular demand! I have taken a quotation, and I have replaced each of the letters with one-, two- of three-digit numbers according to the table below. Can you change it back to letters?

Be careful though, as some sequences of numbers could lead to several words, for instance 31110 could mean CAT (3,1,110), but could equally mean MAD (31,1,10).

233121103  113213030  211  233121103,  13210  10333  113213030  1  3033110  3312  312110103011-1131110  311132.

Puzzle of the Week #6 - Paddocks

Draw fences between some of the posts so that each post is at the junction of exactly three fences.

These fences will divide the field into several paddocks; any paddock whose area is greater than a single triangle will contain a number, which will indicate the area of the paddock that contains it.

The boundary fence is already in place, so any post on the boundary only needs one more fence emerging from it in order to make up its full complement.

For example:

Here is the puzzle: