x is equal to 32 feet, such that the corridor is a little over 4 feet wide.
Solution of the Week #345 - Christmas Star
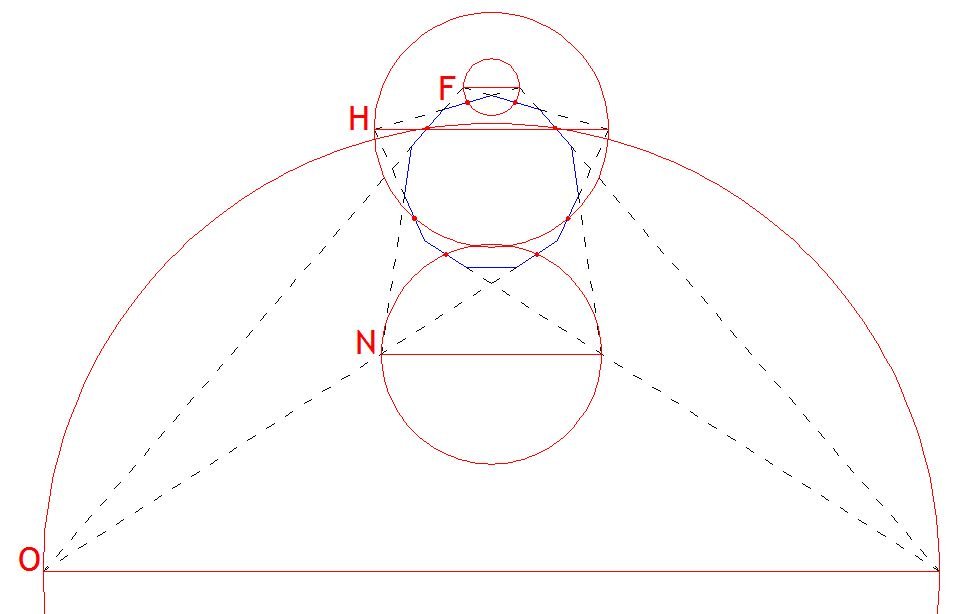
Lines F, H, N and O are all diameters of circles which pass through midpoints of sides of the original hendecagon.
The key insight is that an angle within a semicircle will be a right angle, so we start off with two construction lines at right angles, one collinear with one of the sides of the 11-sided polygon, another passing through the vertex opposite that side. By definition they will intersect at the midpoint of the side of the polygon.
On the left hand side draw extensions from all possible polygon edges that can meet the blue (horizontal) line, and on the right hand side draw extensions from all possible polygon edges that can meet the red (vertical) line (some will go upwards, others downwards). The red intersections are intersection points of extended polygon sides, as the red lines can be mirrored by the red axis. The blue intersections are already intersections of extended polygon sides as the blue axis itself is an extended polygon side.
The intersection points with the main axes can be paired up according to how far they are from the centre of the polygon. By definition any circle with one of these magenta pairing lines as its diameter will pass through the point where the axes meet (as well as a second polygon midpoint which will vary from circle to circle).
None of these pairing lines are horizontal as in the puzzle, but it’s easy to see how for each pairing line, the figure can be rotated such that the line is horizontal. If you do so you will find that the four lines correspond to the lines F, H, N and O in the puzzle.
Solution of the Week #344 - Rectangles in a Quadrant
The simplest way to calculate the areas of the rectangles is probably to complete the circles, with three additional copies of each quadrant, then draw a diameter between two opposite points as shown:
In the first case the area of the required rectangle is 2x^2, and in the second it is 2y^2.
In the first diagram, there is a right triangle with legs 2x and 4x, and hypotenuse 2.
(2x)^2 + (4x)^2 = 2^2
4x^2 + 16x^2 = 4
20x^2 = 4
2x^2 = 4/10 = 2/5
Similarly in the second diagram:
y^2 + (5y)^2 = 2^2
26y^2 = 4
2y^2 = 4/13
So the areas are 2/5 and 4/13 respectively, and their difference is therefore 6/65. Or if you chose to interpret the question the other way, the first rectangle is 30% larger than the second.
Solution of the Week #343 - Making the Infinite Finite
11/18 (0.61111…)
Each term 1/(n(n+3)) can be rewritten as two separate terms:
A/n + B/(n+3)
To find the values of A and B we force them back into a single fraction and make sure it’s equal to the original fraction:
(A(n+3) + Bn)/ (n(n+3)) = 1/(n(n+3))
(A+B)n + 3A = 1
The n term must disappear as there isn’t one on the right-hand side, so A+B=0.
3A=1, so A=1/3, and so B=-1/3
So each term 1/(n(n+3)) is equivalent to 1/3n - 1/(3(n+3)). For example the first term 1/4 is equal to (1/3 - 1/12), the second term 1/10 is equal to (1/6 - 1/15), etc.
This might seem to be unnecessarily complicating the infinite sum, however you might notice that the negative part of each term will appear again as the positive part, three terms later:
(1/3 - 1/12) + (1/6 - 1/15) + (1/9 - 1/18) + (1/12 - 1/21) + (1/15 - 1/24) + (1/18 - 1/27) …
Virtually everything will cancel out. Only the positive parts of the first three terms will remain, and can easily be added together to find the final answer:
1/3 + 1/6 + 1/9 = 11/18, or 0.6111…
If you were to add up successive terms on a spreadsheet you would find that it does indeed approach this sum, but it does so very very slowly. It only reaches 0.6 after about 90 terms, 0.61 after about 900 terms, 0.611 after about 9000 terms, 0.6111 after about 90000 terms etc.
Solution of the Week #342 - Block in the Alley
You can use Pythagoras’ theorem to find the length of the diagonal of the block to be 425cm. This diagonal is simultaneously the hypotenuse of another triangle whose base is 340cm and whose height is the number we are after. Using Pythagoras again we find that the height difference is 255cm.
Solution of the Week #341 - Mastermind
From guess 3, one is in the correct place. It cannot be the initial Red as that would have shown as in the correct place in guess 1. Similarly it cannot be the final purple, as guess 2 would have shown it. So it must be the red in position 2.
Since the first two guesses cover all of the colours, but only show two correct pegs, there must be a colour repeated. It cannot be the red, or else that would have shown in guess 3. It must be one of the colours from guess 2, but since they must occupy positions 1 and 3 in the answer, they cannot be Orange or Purple, as they would have shown as in the correct place in guess 2.
The final answer is therefore Blue Red Blue
Solution of the Week #340 - Infinite Coin Push
All three coins will be at (13,7).
The key to solving this is to compute the x and y coordinates separately. We are given the first three x coordinates, 0, 3, 9 and each subsequent x coordinate will be 3/4 of the previous two less 1/2 of the one before that. Eventually this settles on an x coordinate of 13. Doing the same for the y coordinates will eventually settle on 7.
In general, given starting positions of A, B, C, the coins will converge on: (-2A+B+4C)/3.
Solution of the Week #339 - Envelope Centroid
The centroid of a shape is the weighted average of the centroids of its component parts.
A_1.C_1 + A_2.C_2 = A.C
Where A_1 is the area of the unshaded region, C_1 is the centroid height of the unshaded region etc.
We require C_2, so making that the subject:
C_2 = (A.C - A_1.C_1)/A_2
We can calculate the area and centroid height (A and C) of the overall figure from first principles, as it is simply an equilateral triangle, and we can find A_2 by simply taking A_1 from A.
C_2 = (rt(3)/4 x rt(3)/6 - rt(3)/6 x rt(3)/10) / (rt(3)/12)
C_2 = 3rt(3)/10 =~ 0.5196…
Solution of the Week #338 - Base 4 Riddle
I'm found in socks, scarves and mittens; and often in the paws of playful kittens. What am I?
Wool!
Solution of the Week #337 - Unit Square
When the two free endpoints are 0.414213… (sqrt(2) - 1) away from the lower left / upper right corner respectively, the shaded area will be at a maximum, which will be exactly 3.5 - sqrt(8), or 0.67157…, a little over two thirds.
Solution of the Week #336 - Consecutive Missing Letters
CLAMBERED
FIREFIGHTER
REQUEST
Solution of the Week #335 - Maximum Quotient
11000 / (1 x 1000) = 11
Solution of the Week #334 - Skeleton Cube
When viewed such that the cubes where the spheres are centred are at the top and bottom of the figure, those points are square root of 3 apart. The unit lengths lines from the top and bottom vertices describe the extent of the overlap of the two spheres (they are actually cone shaped but from this angle appear to be equilateral triangles). The circle in the middle of the cube is viewed here edge-on, and so its diameter is 1.
Solution of the Week #333 - Non-seqitur
Since 5 is a prime number, the only way a number can have exactly five factors is if it is the fourth power of a prime number, in which case the factors will be 1, p, p^2, p^3 and p^4.
Therefore, to answer the question we need to find out how many prime numbers lie between the fourth root of 10^4 and the fourth root of 10^6. The fourth root of 10^4 is clearly 10. The fourth root of 10^6 is 10^(6/4) which is 10^(3/2) or 10 x 10^(1/2), in other words 10 x the square root of 10. The square root of 10 is given in the question as about 3.16, so therefore the fourth root of 10^6 is about 31.6.
So the answer we seek is the number of prime numbers between 10 and 31.6, which is straightforward enough to simply count: 11, 13, 17, 19, 23, 29, 31 which gives the answer of 7.
Solution of the Week #332 - Even Binary Puzzle
The highest number that will terminate at 25 is 123:
123 1111011 111 x 1011 7 x 11
77 1001101 1001 x 101 9 x 5
45 101101 101 x 101 5 x 5
25 11001 stop
The highest number that will stop at 32 is 965:
965 1111000101 111 x 1000101 7 x 69
483 111100011 111 x 100011 7 x 35
245 11110101 111 x 10101 7 x 21
147 10010011 100100 x 11 36 x 3
108 1101100 110 x 1100 6 x 12
72 1001000 100 x 1000 4 x 8
32 100000 stop
Solution of the Week #331 - Sixth Powers
All sixth powers are either a multiple of 13 or one away from a multiple of 13:
1 = 13x0 +1
64 = 13x5 -1
729 = 13x56 +1
4096 = 13x315 +1
5^6 = 13x1202 -1
6^6 = 13x3589 -1
7^6 = 13x9050 -1
8^6 = 13x20265 -1
etc.
To check that it works for ALL sixth powers, you only need to check the first 13, since:
(n+m)^a = (n)^a (mod m)
Proof: if you multiply out the left-hand side, one term will be (n)^a, plus several other terms which will all contain m, and therefore be a multiple of m, and not affect its value, modulo m.
In actual fact you only have to look at the first 6, since
(m-n)^a = (-n)^a (mod m), for precisely the same reason.
To be sure that there are no numbers higher than 13 that work, you only need to look at the first couple of sixth powers (and the numbers either side of them) and see what their factors are.
The only numbers that divide into (63, 64, OR 65) AND (728, 729 OR 730) are 1,2,3,4,5,7,8,9,13.
13 is the highest of this list, so as long as it proves to be a valid solution, it will be the highest such solution.
Solution of the Week #330 - Self-Assembly
Authors of detective fiction:
(RAYMOND) CHANDLER
(AGATHA) CHRISTIE
(DASHIELL) HAMMETT
(JO) NESBO
(RUTH) RENDELL
(MICKEY) SPILLANE
Solution of the Week #329 - p+2=sp
Since we are told that a pair of 3s are amongst the prime factors of n, the semiprime 9 is a factor, and since 9 is 2 greater than a prime, 7 is also a factor. So another semiprime factor is 21, therefore 19 is a prime factor. Of the semiprime factors involving 19, 133 is 2 greater than a prime number, so 131 is also a prime factor of n. Of the semiprimes involving 131, there are none that are 2 greater than a prime, so we can stop there.
n is therefore 3x3x7x19x131 = 156807.
There could be other factors, for instance if 41 were also a prime factor, the rule would still be satisfied, since 41 in not 2 less than a semiprime, and each of the semiprimes involving 41 would not be 2 greater than a prime, so 156807 is merely the smallest.
For the second challenge, we need to introduce another prime factor, as small as possible.
It cannot be 2, as that would imply 4 divides too, but we know we can’t have any more repeat prime factors.
If it was 5, that implies 13 is also a factor, so we’ll put that to one side.
If it was 11, 31 would also be a factor.
13 implies 5 is a factor, as we’ve already seen.
If 17 is a factor, none of the semiprimes formed with it are 2 greater than a prime, and 17 itself is not 2 less than a semiprime, so we can stop there.
Therefore multiplying the previous answer by 17 gives the next smallest: 2665719.
Solution of the Week #328 - Binary Determination
Solution of the Week #327 - False Conjecture
The 58th number: 64,320,987,654,320,987,654,320,987,654,320,987,654,320,987,654,320,987,654,321
is the first in the sequence to be prime.
The 40th number: 44,320,987,654,320,987,654,320,987,654,320,987,654,321
is tempting as it doesn’t have any prime factors smaller than 78 million, but it is in fact composite.
Several others only have two prime factors.