A right-angled triangle has a height of 4, and one its sides is 3 more than another as shown. What is the length of the base?
Puzzle of the Week #454 - Heptagon Circle Maximisation
Cut out a heptagonal ‘bite’ from a circle. The bite is four sides of a regular heptagon. The remaining arc length should be constant, and you wish to maximise the area. Below are two figures towards the extremes: a small circle with a small heptagon bite, or a far larger circle, but where the heptagon takes most of that area. In between these two figures there will be a point where the area is at a maximum, but how to construct it?
I had previously solved a far simpler version of this, where the bite was formed by two edges of a square. The optimum in that situation was for the inner vertex of the square to lie on the centre of the circle. In other words the resulting figure would be a three-quarter-circle. It turned out on further examination that the fact that the two lines of the square met at right angles was not important, but the fact that the lines were equal WAS. So if the bite was formed of two identical lines meeting at ANY angle, the maximum area for that angle is achieved when the vertex lies on the centre of the circle:
How can you use this information to construct the maximum area in the case of the heptagon?
Puzzle of the Week #453 - The Long Game
I have 7 copies each of 14 cards labelled A-N. Each day I try to play a card. I cannot play the same letter as the previous day. In addition if I played a letter for the nth time, the next day I cannot play another letter for the nth time. If I cannot play a card I must take a day off, but the following day I can play whatever card I want.
How many days will it take me to play all of the cards?
Puzzle of the Week #452 - Find the Radius
Within this right-angled triangle a rectangle is drawn. Four identical blue circles and two identical red circles are drawn, tangent to each other, the rectangle and the triangle as shown. If the radius of the red circles is 9, what is the radius of the blue circles?
Puzzle of the Week #451 - Answer Sequence
Solve these clues and place the answers in the correct order:
Santa’s little helper
Long term prisoner
Dossier
Lightning bug
Interleaf (playing cards)
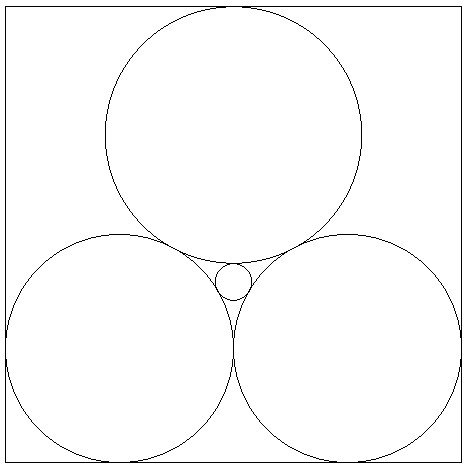
Puzzle of the Week #450 - Small Circle
Four circles are drawn in a unit square as shown. The two lower circles are the same size. What is the radius of the small circle, as a fraction?
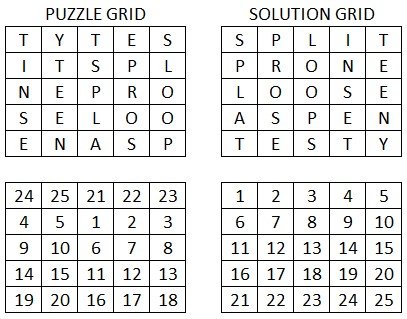
Puzzle of the Week #449 - Swap Grid
I have taken a square of five letter words and scrambled it in a particular way: each letter was moved across 2 and down 1 from its position in the solution grid, which is made clearer by the corresponding number grid below.
This is a logic puzzle, not a word puzzle, as is apparent from the fact that I’ve given you the solution grid as well as the puzzle grid.
Your task is to figure out the least number of swaps required to turn the puzzle grid into the solution grid, with each swap simply being to take any two letters from anywhere in the grid and swap them.
If you attempted this on the number grid, you would require 20 swaps, however in the letter grid you can take advantage of the fact that some letters are repeated to reduce the number of swaps.
A bonus question if you feel like it, is to work out how many swaps you can make that, while advancing towards to solution within the minimum number of swaps, don’t actually solve any letters. To explain what I mean, in the number grid if you were to swap the 1 and the 15, neither would be in its final position, but you have advanced the solution in the sense that it can now be solved in 19 further swaps.
Puzzle of the Week #448 - 2023 2024 Puzzle
What is the value of:
Puzzle of the Week #447 - New Order
The following list of words are in alphabetical order. Change them into a different order that also has some reason behind it but has nothing to do with the alphabet.
Antenna
Freighter
Lioness
Network
Zaniness
****Thank you for trying to solve my puzzles this year. This is the last for 2023 as I take a break over the Christmas period. I’ll be back in the new year.****
Puzzle of the Week #446 - Pentagon to Square
Here is a pentagon with five equal sides, however its angles are not all equal. Two of them are right angles as shown. Can you dissect this pentagon into just three pieces and reassemble them to form a square?
Puzzle of the Week #445 - Functional Equation
2*f(3/(3-x)) – f(x) = 135*x
What is the value of f(4)?
f(x) is a function of x. The above is a ‘functional equation’, where f() of more than one different value appears as an unknown. It may look intimidating, but if you approach it in the right way, it is solvable without any advanced mathematics. As a slight push in the right direction, see what happens if you let x=4.
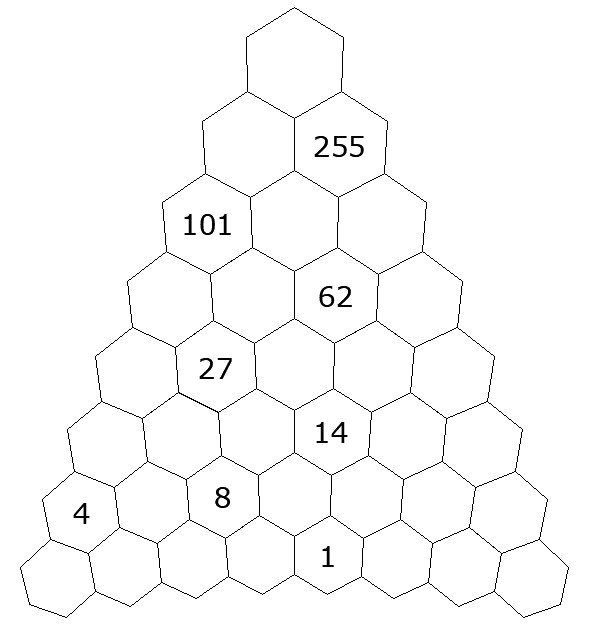
Puzzle of the Week #444 - Pascal's Ladder
In this grid, each number needs to be the sum of the two numbers immediately below. Once complete, the bottom row will spell out a famous date in English history.
Puzzle of the Week #443 - Find the Value
There is only one real value which satisfies this equation, what is it?
(2x+3)(3x+4)(4x+5)=11
Puzzle of the Week #442 - Triangle on a Square
A triangle DEF sits atop a 24 x 24 square ABCD. The triangle is special for a couple of reasons. E D and C are collinear, and E F and B are also collinear. In addition, the area of triangle DEF has the same value as its perimeter. What is that area?
Puzzle of the Week #441 - Puzzle 441
It is possible to write the numbers 1 to 441 in a particular order such that the sum of every consecutive pair of numbers is either 321, 442, or 763. For instance, 400 might be followed by 42 or 363.
When you do this, what numbers are at the start and the end of the sequence?
And for bonus points, what number would be in the exact centre of the sequence?
Puzzle of the Week #440 - Semicircles in a Hexagon
This is a regular hexagon with unit length sides. The radius Ra is obviously equal to 0.5, but the other radii are all different. What is the value of radius Re?
Puzzle of the Week #439 - Odd Primes
The numbers p, q, r and s are odd prime numbers such that:
p+5 is divisible by q
q+6 is divisible by r
r+7 is divisible by s
s+8 is divisible by p
What are p, q, r and s?
Puzzle of the Week #438 - parkrun Density
I have 17 parkruns within 17 miles from my house.
Assuming the density is broadly uniform, if I calculate the same stat but in kilometres, such that I have n parkruns within an n kilometre radius, what is a good estimate for n?
(There are ~1.61km in a mile).
a) 11
b) 17
c) 22
d) 27
e) 44
Puzzle of the Week #437 - Rugby Scores part 2
We saw last week how the number of ways of reaching a particular score by adding 3s, 5s and 7s can be found using the recurrence relation:
a(0)=1, a(n)=a(n-7)+a(n-5)+a(n-3) for n not equal to 0.
Now we go slightly abstract and just look at, for all the values of a(n) for n greater than or equal to 0, the parity (odd or even) of each value.
I’ll give a simpler example just to be clear. If a(n)=a(n-2)+a(n-1) and a(0)=1, you get this familiar sequence: 1,1,2,3,5,8,13,21,34,55, etc. Just looking at the parity we get: OOEOOEOOEO etc. It seems to be the case that two-thirds of the numbers in that sequence are odd, and indeed that is the case.
The rugby sequence begins 1,0,0,1,0,1,1,1,2,1,3,3,3,6,5,8,10,11,17…
Which is: OEEOEOOOEOOOOEOEEOO etc
If you continue that sequence forever, what proportion of the values are odd?
Puzzle of the Week #436 - Rugby Scores
As the Rugby World Cup is currently ongoing I thought I’d do a puzzle based on the scoring system. A kick (drop goal or penalty) is worth 3 points, an unconverted try is worth 5 points, and a converted try is worth 7 points.
Some scores are impossible to reach: you can’t get 1, 2 or 4.
8 is the first score that’s achievable in two ways, as long as we say that ‘3 then 5’ is different from ‘5 then 3’.
In how many ways is the score ‘23’ achievable?