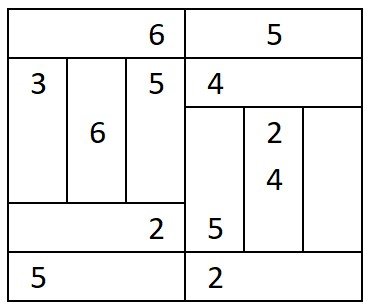
If Friday 18th April is at the start, what date is at the end?
Puzzle of the Week #356 - Counter Game 2
In a similar vein to my previous puzzle Counter Game, there are a number of counters on the table, but this time you can either remove 2 or 7 of them on each turn. For instance if there were 11 counter there are three solutions: 2,2,7; 2,7,2; 7,2,2; (as before removing 7 then 2 is distinct from removing 2 then 7). Some numbers of counters have no solution, for instance if there are 5 counters you cannot remove them all.
If the number of counters is high enough, there are always more different ways to remove all the counters than to leave one counter behind, but this is not true for some smaller numbers, for instance if there were 12 counters there is only one way of removing them all (2,2,2,2,2,2), but as we have seen, three ways of removing 11 and leaving 1 behind.
What is the highest number of counters, for which there are fewer ways to remove them all than to leave one remaining?
Puzzle of the Week #355 - Human Logic
Construct a list of 9 common five-letter words, such that with every new word in the list uses at least one letter that you haven’t used in any of the preceding words. Just to make it a little more difficult, you may only use the letters in the words HUMAN LOGIC.
Puzzle of the Week #354 - Counter Game
I have 16 counters. On each turn I either remove 1, 2 or 3 counters until there are no counters left.
I could remove 2 counters eight times, or I could remove five lots of 3 counters then a single counter, or I could remove 3, 2, 2, 1, 3, 1, 1, 1, 1, 1, or any number of different ways.
Well in fact not ‘any’ number of different ways. Your task is to find out exactly how many ways there are. Note: the same combination but occurring in a different order counts as different ways, for instance, there is only one way using 2 eight times, but there are six ways involving five 3s and a 1.
I’ve chosen the number of counters to be 16 because the total number of ways is the square of a prime number. This fact doesn’t particularly help you, except for checking whether or not you are correct.
How many different ways are there?
Puzzle of the Week #353 - Odd Shape
Within this figure are three squares and three triangles. The edge length of two of the squares is 2 and 3 units respectively. What is the area of the overall shape?
Puzzle of the Week #352 - Construct-a-Wordle
You have probably seen this game going around the interwebz:
The object is to guess the secret word. For each guess you make, you will be told if a letter is correct (green), or if it does occur in the secret word, just not where you’ve placed it (yellow), or if it’s not in the secret word at all (white).
Not one to miss a bandwagon, I thought I’d make a variation on the theme:
In the Wordle below, the letters for the first four guesses are given, and are above the correct column. The puzzle in threefold: firstly reconstruct what the first four guessed words were; secondly, place the four words in the correct order in the grid; thirdly, use the green, yellow and white squares from the first four rows to work out what the actual secret word should be.
Puzzle of the Week #351 - Secret Message
Complete the final column to find a secret message:
Puzzle of the Week #350 - Three Sisters
There are three sisters, all of different ages, but all sharing a birthday.
At some point in the distant past, the older sister’s age was a cube number and her sisters’ ages were both prime numbers.
Now, some time later, the older sister’s age is again a cube number, and the younger sisters’ ages are again both prime numbers.
How old are they all?
Puzzle of the Week #349 - Fiendish Sudoku
In the following sudoku, within each and every 3x3 ‘box’, the rows add up to 9, 15 and 21 and the columns add up to 9, 15 and 21 (in some order).
For instance one box might be:
2 3 4
7 5 9
6 1 8
as the row totals are 9, 21 and 15, and the column totals are 15, 9 and 21.
Other than that, usual sudoku rules apply: the numbers 1 to 9 appear once each in every row, column and box.
Starting tip: list all the possible ways of totalling 9 then look at the central box.
Puzzle of the Week #348 - Brickdoku 2
Each row and each column should contain every number from 1 to 6. Additionally, the numbers in each ‘brick’ should add up to a multiple of 3.
Puzzle of the Week #347 - Brickdoku
Each row and each column should contain every number from 1 to 6 (1 to 4 in the example). Additionally, each ‘brick’ should contain one even number and one odd number.
Puzzle of the Week #346 - Corridor
There is a building whose plan view is an equilateral triangle, x feet along each side. The building is divided into an internal room and a corridor along two sides of the building, such that the area of the corridor is exactly the same as the area of the internal room. The width of the corridor is sqrt(6x) - sqrt(3x) feet. What is the value of x?
Puzzle of the Week #345 - Christmas Star
I have taken a regular hendecagon (11-sided polygon) and added extensions to each of the sides so that they intersect as shown. Wherever it is possible to connect two of these intersection points with a horizontal line I have done so, and denoted them A to P. (Except for the magenta dashed line passing through the horizontal side of the hendecagon, which has several intersection points on it, but can be ignored for the purposes of this puzzle).
Some of these lines A to P have a very curious property, that if you form a circle whose diameter exactly coincides with said line, the circle will pass exactly through the midpoints of two of the sides of the original hendecagon.
Can you list all those lines which have this property?
Puzzle of the Week #344 - Rectangles in a Quadrant
There are two ways to draw a rectangle whose length is twice as long as its width, within a quarter circle of radius 1, such that all four corners lie on the boundary of the quarter circle.
One of the rectangles has an area greater than the other, but by how much exactly?
Puzzle of the Week #343 - Making the Infinite Finite
What is the value of the following sum?
1/4 + 1/10 + 1/18+ 1/28 + … continuing forever,
where each denominator is each successive natural number, n, multiplied by n+3.
Puzzle of the Week #342 - Block in the Alley
A rectangular block measuring 375cm x 200cm is positioned in a 340cm wide alleyway as shown. How much higher is the left corner than the right?
Puzzle of the Week # 341 - Mastermind
A code of three coloured pegs is selected from Red, Yellow, Green, Orange, Blue and Purple.
Guess 1: Red Yellow Green: one correct but in the wrong position
Guess 2: Orange Blue Purple: one correct but in the wrong position
Guess 3: Red Red Purple: one correct, and in the correct position
Solution: ?
Puzzle of the Week #340 - Infinite Coin Push
We used to play a game back when I was at school. We would start with three coins placed widely apart on a table. The first player would give one of the coins a shove, so that it would pass between the other two. Then the next player would try to do the same, starting from the current position, but using one of the other coins. This would continue until one player would inevitably fail to get the coin between the other two.
I’m now imagining an idealised version, where the coins are single points, and on each turn the coin passes through the exact midpoint of the positions of the other two coins and continues a further 50%. So to begin with, the coins are at (0,0) (3,9) and (9,3) respectively. The midpoint of the initial positions of coins B and C is clearly at (6,6), so coin A will travel from (0,0) to (6,6) and then continue another 50% to come to rest at (9,9). Next it is the turn of coin B. Coin B must travel to the current midpoint of coins A and C and extend another 50% distance to find its new position. The coins take turns in the order A, B, C, A, B, C etc
The diagram below shows the first two moves of each coin.
After an infinite number of moves, where will each of the three coins be?
Puzzle of the Week #339 - Envelope Centroid
ABC is an equilateral triangle. If I tell you that the area of the unshaded region is sqrt(3)/6 and that the centroid (centre of gravity) of the unshaded region is sqrt(3)/10 above AC, how far above AC is the centroid of the shaded region?
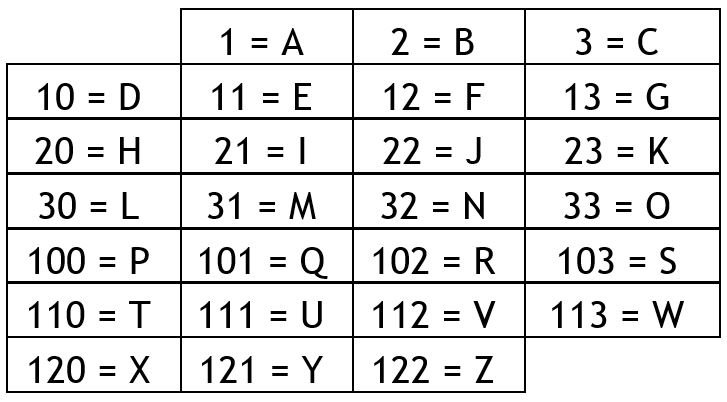
Puzzle of the Week #338 - Base 4 Riddle
I have taken a riddle, and I have replaced each of the letters with the numbers that denote their position in the alphabet. However, I have used the base 4 number system.
Be careful, as some sequences of numbers could lead to several words, for instance 31110 could mean CAT (3,1,110), but could equally mean MAD (31,1,10). Can you decode the riddle and then solve it?