In Elbonia they only have three denominations of coins: 15 ELB, 21 ELB and 35 ELB. Although each pair of these coins have a common factor, all three do not. This means that if the value is high enough, any value can be expressed exactly with no change required. But what is the highest amount that cannot be expressed exactly?
Puzzle of the Week #225 - Six Integers
x^2 = a^2 + 4b + 1
y^2 = b^2 + 4c + 1
z^2 = c^2 + 4a + 1
a, b, c, x, y, z are all positive integers
a > b > c
x > y > z
What are the values of the six integers?
(There is a really neat algebraic trick you can use here. First see if you can calculate x in terms of a).
Puzzle of the Week #224 - How Many Coins
I have a number of coins. I throw them all, count how many heads and how many tails and multiply those two numbers together. I calculate what the expected (average) answer should be and discover it is exactly three times the number of coins. How many coins do I have?
(For instance if there were three coins, there are eight possibilities:
HHH TTT HHT HTH THH TTH THT HTT
The first two result in 3 x 0 = 0, and the other six result in 2 x 1 = 2, so the average answer is 1.5)
Puzzle of the Week #223 - Winston Churchill
I have a six letter word, a clue to which is: ‘Something Winston Churchill often is’.
If I change the first letter of my word to the letter that follows it in the alphabet, and then reverse the entire word, I get a new word.
What was my word?
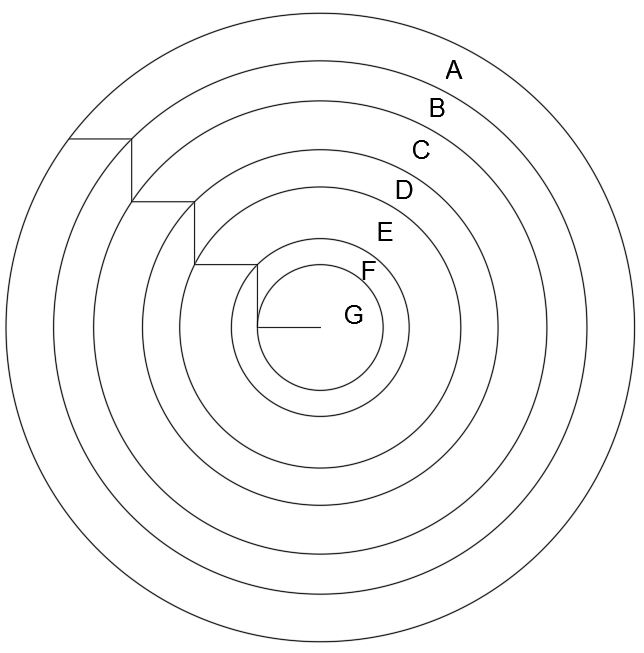
Puzzle of the Week #222 - Staircase Rings
In the following diagram, the ‘staircase’ is made up of horizontal and vertical lines of equal length. The ends of these lines determine the radius of each of the rings, whose shared centre is the end of the final horizontal line.
If the overall shape has an area of 100, what is the area of each of the individual regions A to G?
Puzzle of the Week #221 - Quotation Wordsearch
A quotation has been hidden in the large grid below. The first word can be read off (left, right, up, down, but not diagonally), and its letters eliminated. Later words in the quotation may not be made of consecutive letters until the letters of previous words have been eliminated. All the letters in the grid will be used exactly once then eliminated.
As an example, the phrase ‘In the nick of time’ has been hidden in the example grid:
“4, 3, 6, 3, 8: 3, 8, 3, 5, 9. 3, 2, 3, 4, 5, 3, 6”
Puzzle of the Week #220 - 23 Days
If we count a workday as a day that is not Saturday or Sunday and is not a Bank Holiday, the most you will see in a given calendar month is 23. This happens twice in 2019: July and October. In the UK there are Bank Holidays at New Year, Easter, May, August and Christmas. Is it possible for a calendar year to have no months with 23 workdays?
Puzzle of the Week #219 - Four Leaf Clover
Four identical pieces forming a square with a four-leaf-clover shaped hole can be rearranged (after flipping half the pieces) into a rhombus with three circular holes. The shorter diagonal of the rhombus is the same as the side length of the square.
Rounded to the nearest whole number percentage, what proportion of the square is shaded?
Puzzle of the Week #218 - Fast Flowing River
Grace and Ruby live in a house next to a fast flowing river. One day they decide to travel a few miles down the river and then return home. Grace is on foot, jogging along the riverbank at a speed of 5mph. Ruby takes the boat, which can travel at 9mph relative to the current of the river. They both set off at the same time, turn around at the same spot and arrive home at the same time. How fast was the current of the river?
Puzzle of the Week #217 - Identical Twins
Phyllis and Dilys are identical twins. They are each independently given the same 4-digit number.
Phyllis takes the number and converts it from decimal (base 10) to base 4, and writes down the 6-digit result.
Dilys simply writes the first and last digits of the number followed by the number in its entirety.
They are astonished to find that they have both written down the same 6-digit number!
What was the original number?
In other words, which number ABCD, when converted from decimal to base 4 becomes ADABCD?
Puzzle of the Week #216 - Four Semicircles in a Rectangle
Four semicircles are arranged around the edges of a rectangle. What are their respective radii?
This is a great deal more difficult than ‘Three Semicircles in a Square’. If it helps I can tell you that there is exactly one solution, and that each of the radii are rational numbers (so if you find it useful – and I’m not at all sure you will - you can scale the whole thing up by some factor, solve as a Diophantine set of equations, and scale back down again). I myself found this very difficult to solve, so if you discover a route to the solution that is not too difficult, I would be interested in knowing it.
Puzzle of the Week #215 - Three Semicircles in a Square
Three semicircles are arranged around the edges of a unit square. What are their respective radii?
Puzzle of the Week #214 - Travelling Salesman
A travelling salesman needs to visit each of the black squares in turn and return to where he started. He can choose to start wherever he wishes. He traces a zero-thickness path, can travel at any angle (this gridlines are only a reference) and doesn’t need to go to the middle of each black square, it is sufficient for his route to touch a corner or an edge. If each small square measures 1 x 1, what is the length of the shortest route?
Puzzle of the Week #213 - Collate
Given a string with three each of three different letters ordered thus:
A A A B B B C C C
It is possible through a series of three moves to change the order into:
A B C A B C A B C
A ‘move’ consists of taking a section of the string and reversing the order of the items within it. The brackets show the section to be reversed in the subsequent move:
A(AABB)BCCC -> ABBA(ABC)CC -> AB(BACBAC)C -> ABCABCABC
Using the exact same idea, how many moves will it take to change between the following?
A A A A A B B B B B C C C C C D D D D D E E E E E
A B C D E A B C D E A B C D E A B C D E A B C D E
Puzzle of the Week # 212 - Infinite Sum
The convergent sum of the following infinite sequence, in its simplest terms, is a fraction with a square number on the top and a factorial number below.
1/7 + 1/16 + 1/27 + 1/40 + 1/55 + 1/72 + … + 1/n(n+6) + …
What is it?
Footnote: the partial sum converges extremely slowly, such that if you add the first million terms you will only get the first 5 decimal places. However there exists a very nice trick to allow you to work out exactly the number the infinite sum converges upon (without having to do an infinite number of calculations!).
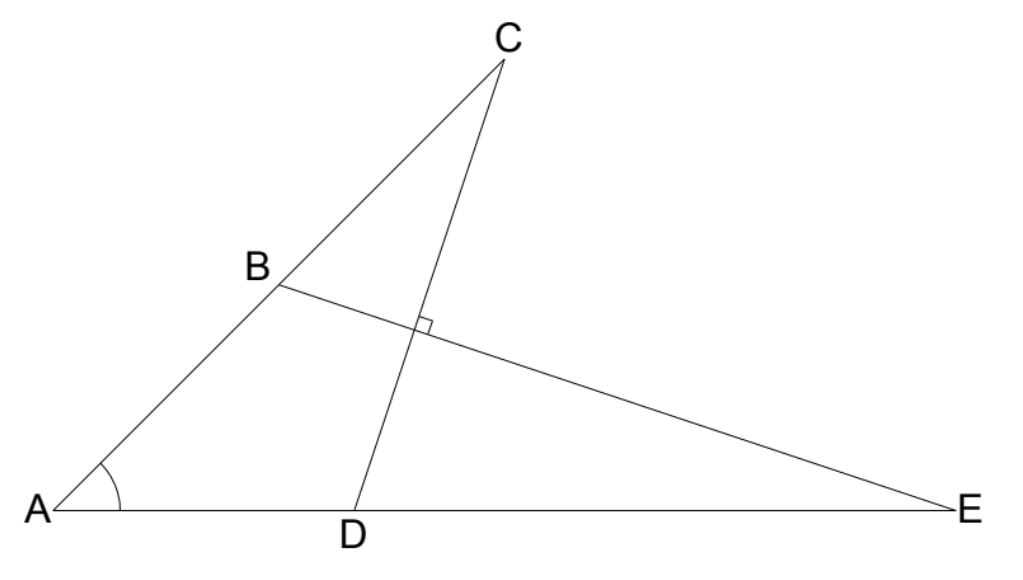
Puzzle of the Week #211 - Angle
B is the midpoint of AC
D is one third of the way along AE
CD is perpendicular to BE
AE is (√2) times the length of AC
What is the angle at A?
Puzzle of the Week #210 - Return Journey
The towns of Abbottsville, Beresford and Christchurch all lie on one straight road. I embark on a journey from Abbottsville, through Beresford, to Christchurch, and back the same way. Each day I cover 1 mile more than the day before. It takes me 10 days to travel from Abbottsville to Beresford, 11 days to travel from Beresford to Christchurch and 12 days to travel from Christchurch (through Beresford) to Abbottsville.
What are the distances between the towns?
Paddocks App News!
The open beta has now started 🎉
Also, there’s now a little trailer on the store page (link to the trailer: https://www.youtube.com/watch?v=is8n293Z_zs).
Unfortunately, Google doesn’t offer Instant Apps for beta versions, so at the moment there is no free
demo available. We can hopefully get that sorted in the next few days.
Moritz Neikes has done a tremendous job with the app, thank you Moritz!
Puzzle of the Week #209 - Coin vs Dice
Which of the following scenarios should on average* take the most throws:
Repeatedly tossing a coin until you have seen at least 6 heads and at least 6 tails, or
Repeatedly throwing a dice until you have seen each of the numbers 1 to 6 at least once each?
*(simple arithmetic mean)
Puzzle of the Week #208 - Factorials Again!
Find a set of three (different positive whole) numbers whose sum is 6! And whose product is 9!