Puzzle of the Week #182 - The Rickety Carousel
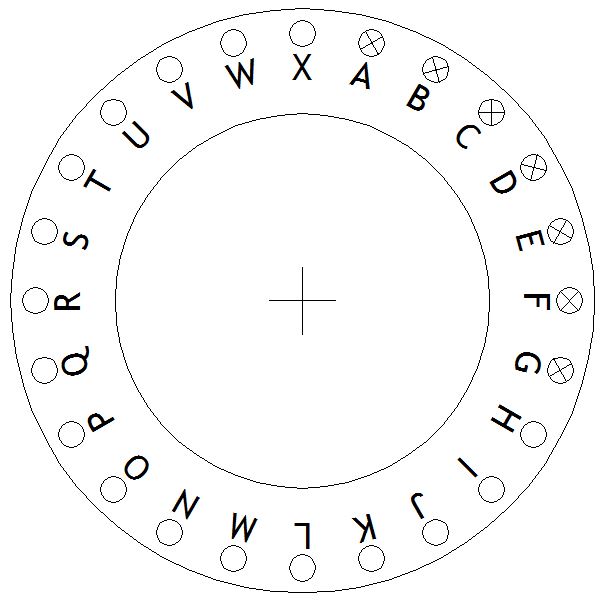
There is a rickety old carousel, with 24 horses equally spaced around the edge of a disc. There are at least two things wrong with it: one is that the horses in positions A, B, C, D, E, F and G are broken and not safe to ride; another is that the carousel needs to be perfectly balanced around the centre of the disc, otherwise it won’t go round. This means that when there are two children wishing to ride, they would have to be positioned in diametrically opposite positions, eg, A and M, in order that the centre of gravity is at the centre of the disc. If there were three children they could be at positions A, I and Q.
On this particular day, nine children wish to ride the carousel. Where do they need to be positioned such that the centre of gravity is at the centre of the disc, and that positions A to G are unoccupied?
Puzzle of the Week #181 - Number Hunt: Four Digit Product
Find a four digit number ABCD such that ABCD x ABC x AB x A = 369,457,740
Bonus Puzzle - Merge In Turn
Bonus Puzzle - Ladders in the Alleyway
Puzzle of the Week #180 - Letter Wall
Two letters of the alphabet are chosen at random. What is the probability that the bricks that correspond to those letters are adjacent in this wall:
Puzzle of the Week #179 - Reducing the Irreducible
The fraction 1174/5063 cannot be reduced further in the usual way, however it can be expressed exactly using only six digits instead of eight.
How?
Puzzle of the Week #178 - Tangent Curve
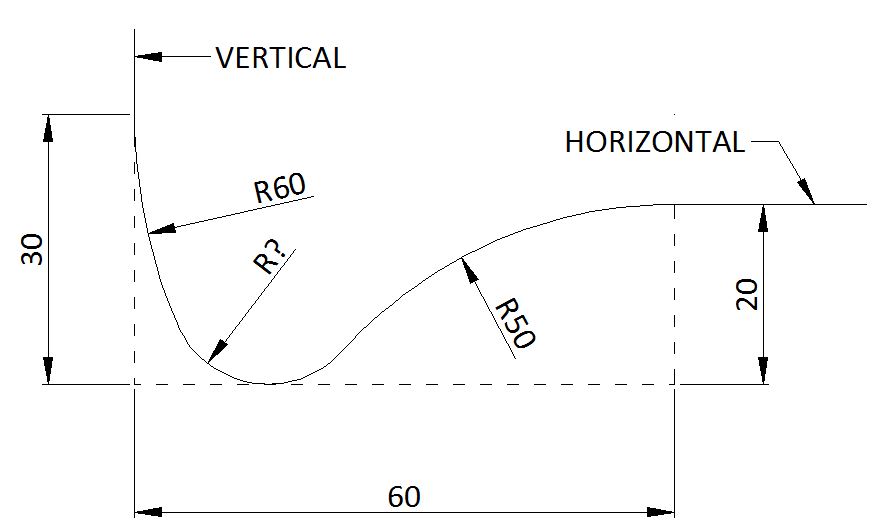
The line begins in a vertical downward direction, transitions into an arc of radius 60, then into another arc with a tighter radius, which just touches the horizontal dashed line. Then there is an arc of radius 50 in a clockwise direction, then a horizontal line. At each transition between line and arc or arc and arc the tangents are continuous.
What is the missing radius?
Puzzle of the Week #177 - Skyscrapers and Empty Lots
Each of the 25 squares contains either a building of height 1, 2, 3 or 4, or an empty lot. Each row and each column contains exactly one of each of those.
The numbers in the twenty ‘vantage points’ around the edge denote how many buildings you can see looking along that particular row or column, so for instance if the 2 building was closest, followed by 1, 4 and 3 in that order, the vantage point would say 2, as you can see the 2-building and the 4-building, whereas the 1-building and 3-building are hidden behind taller buildings.
Here’s an example (with only 1, 2 and 3 height buildings) which might make it clearer, followed by the puzzle itself:
Puzzle of the Week #176 - Nine Point Circle
You might be familiar with the famous ‘Nine Point Circle’ theorem, which says that for ANY triangle the 3 midpoints (shown below in red), the 3 perpendicular feet (shown in green), and the 3 points midway between the each of the vertices and the orthocentre (shown in blue), will all lie on a circle. (Of course for an equilateral or isosceles triangle some of these points will coincide). But I have discovered there is something quite special about the 9 points of a triangle with angles 45, 60 and 75.
What is so special?
The figure is to scale so you may be able to guess the answer.
Puzzle of the Week #175 - Out Standing In My Field
I’m standing in a rectangular field. I am 34m from the top left corner and 62m from the bottom right corner. I am an equal distance from the other two corners: what is that equal distance?
Puzzle of the Week #174 - Rectangle Area
The AREA of each of the eight squares is 26. What is the area of the rectangle that surrounds them?
Puzzle of the Week #173 - Tournament
There are 16 teams in the knockout stages of a football tournament. For the sake of argument, say that each team has a distinct ranking from 1 (best) to 16 (worst), and that in any individual match, the better team will always win and progress to the next round.
The first round matches are randomly arranged, and the eight winners of those matches are randomly arranged in four matches in the quarter final etc.
Which of the following scenarios is more likely:
The 2nd ranked team is knocked out before the semi-finals, or
The 7th ranked team progresses at least as far as the semi-finals?
Puzzle of the Week #172 - Wordwall
Reassemble this word wall using the bricks provided. Unfortunately the bricks that go in the positions marked with an asterisk are missing, and must be reconstructed.
It may actually be useful to print and cut out the pieces.
Puzzle of the Week #171 - Isosceles Triangle
The large isosceles triangle can be dissected into 12 smaller isosceles triangles as shown.
What is the angle at the top of the large isosceles triangle?
Puzzle of the Week #170 - Football Squad
A squad of 20 players (3 goalkeepers and 17 outfield players) splits into two equal teams for a training match (with any unchosen players reduced to spectating). Each team must have exactly one goalkeeper, but otherwise the players are entirely interchangeable.
It is calculated that there are a little over 5 million distinct* ways to select the teams.
*(so, for instance, if it were three-a-side, ABC v DEF would be the same as FDE v BCA).
How many players on each team?
Puzzle of the Week #169 - Word Jigsaw
Seven identically-shaped jigsaw pieces fit into the grid to form words in horizontal and vertical directions. Unfortunately one of the seven pieces has been lost. Can you place the given pieces in their correct positions within the grid and reconstruct the final missing piece?
Puzzle of the Week #168 - Number Hunt
I have a 6 digit number ‘abcdef’ such that the digits a, b and c are all odd and d, e and f are all even. If I multiply my number by 5½ I get ‘defabc’.
What is my number?
Puzzle of the Week #167 - Anagrhymes
It’s been a while since I made a word puzzle, so here is one I hope you’ll like:
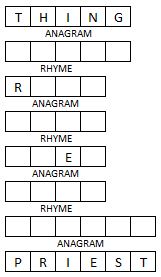
Via a series of steps, change from one word to another, firstly changing to an anagram of the previous word, secondly to a word that rhymes with the previous word, and subsequently alternating between the two types of changes.
For instance if you wanted to change from CHAR to CHARM you could change CHAR to ARCH (anagram), then ARCH to MARCH (rhyme), then MARCH to CHARM (anagram).
Can you change from THING to PRIEST:
Puzzle of the Week #166 - Cubic Conundrum
If
(x + 1/x) = 7
what is
(x^3 + 1/x^3) ?
This being a puzzle rather than just a maths problem, there is of course a way to solve it without having to go through the messy business of working out what x is equal to. You might even want to let (x + 1/x) = A and then express (x^3 + 1/x^3) purely in terms of A.