Puzzle of the Week #62 - Tenpin Bowling

The object of this game is to try to score as highly as possible by using letters in a given rack to form words. Just like in real ten pin bowling, you have a maximum of two attempts at each rack.

If you get a ten-letter word, that is a Strike and is worth 20 points.

If you find two words that between them use each of the ten pins once each, that is a Spare and is worth 15 points.

Any fewer than that, just total up the letters used to give your point total. So if you find a five-letter word and a three-letter word, that rack will have scored you 8 points.

I have randomly generated the racks by drawing 50 scrabble tiles out, discarding only the blanks (unlike the previous outing of this puzzle, where I tweaked it so that at least a spare was achievable on each rack - this way I can legitimately take part myself).

What is the highest total you can achieve over the five racks?

Puzzle of the Week #61 - Power Play

61 raised to the power of 61

or 61 61’s all multiplied together,

or 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61 x 61

is a very large number, with 109 digits altogether.

What are the last three digits?

Puzzle of the Week #60 - Countries

1: Which country’s name, when you insert ‘GRA’ in the exact centre, becomes a common English word?

2: Which country’s name ends with the letter H?

3: Which country’s name, when you insert ‘OR’ in the exact centre, becomes a common English word?

4: Apart from Belgium, which European country’s name ends with the letter M?

5: Which country’s name is an anagram of the name of a Hollywood actress most famous in the 1990s?

Puzzle of the Week #59 - Matching Circles

I have a triangle with a strange property. I find that when I draw a line from the top corner to the base that is precisely 60cm long, the incircles I can draw in the two parts are exactly the same size. The distance between the centres is exactly 24cm.

What is the length of the base of the triangle?

Puzzle of the Week #58 - Triples: Actors

I have taken ten 9-letter surnames of famous actors and actresses, split them into three-letter chunks, and mixed them up. Your task is to reassemble them.

ARD     BLA     CAS     CHE     CLI     DEP     ELD     ETT     FAI     FFE     GER     HOL     ICH     IER     IEU     KOV     LAN     LWE     MAL     MAN     NCH     NIC     NKS     RAD     RBA     SFI     SON     TER     VAL     ZEL

Puzzle of the Week #56 - Ten Pin Bowling

The object of this game is to try to score as highly as possible by using letters in a given rack to form words. Just like in real ten pin bowling, you have a maximum of two attempts at each rack.

If you get a ten-letter word, that is a Strike and is worth 20 points.

If you find two words that between them use each of the ten pins once each, that is a Spare and is worth 15 points.

Any fewer than that, just total up the letters used to give your point total. So if you find a five-letter word and a three-letter word, that rack will have scored you 8 points.

What is the highest total you can achieve over the five racks?

 

 

Puzzle of the Week #53 - Quotebreaker

I have taken a quotation, and I have replaced each of the letters with one-, two- of three-digit numbers according to the table below. Can you change it back to letters?

Be careful though, as some sequences of numbers could lead to several words, for instance 31110 could mean CAT (3,1,110), but could equally mean MAD (31,1,10).

This particular quotation is from the mathematician George Polya, and explains very succinctly why I enjoy puzzles.

1 13102111110 102110333311211102121 103333011211103 1 13102111110 100102332301131, 2111110 110201110211 21103 1 1310212132 3312 102110333311211102121 2132 1102011 1033330111110213332 3312 132121 100102332301131. 12133111102 100102332301131 311121 211 31331011103110, 2111110 2112 21110 3201303011321311103 12133111102 3111102213310321110121 13210 2102213213103 213211033 100301121 12133111102 213211211321102111211 1213111301102111103, 13210 2112 12133111 103333011211 21110 2121 12133111102 3311332 3111132103, 12133111 311121 1112010011102211132311 1102011 1101132103213332 13210 11322233121 1102011 110102211113110020 3312 102110333311211102121.

 

Puzzle of the Week #52 - Seven Towns

Norton lies 100 miles due north of Sutton.

Middleton is exactly halfway between Norton and Sutton.

Middleton is also halfway between Acton and Easton.

Barton is halfway between Acton and Middleton.

Weston is halfway between Barton and Norton.

Weston is due west of Easton.

The distance from Norton to Barton is the same as the distance between Acton and Sutton.

What is the distance from Weston to Easton?

Puzzle of the Week #51 - Pentominoes

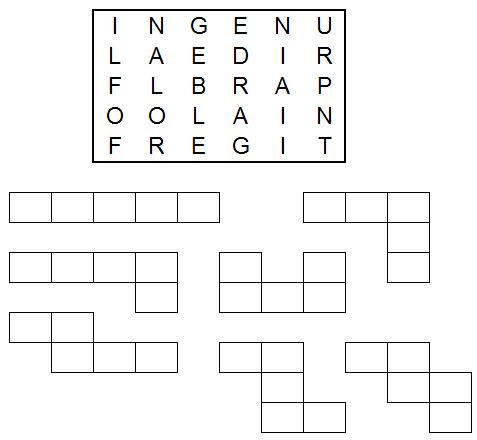
Divide up this grid of 30 letters into six five-letter words. Each word will be in the shape of a pentomino, specifically a pentomino that doesn't branch off or curl all the way around and contact itself.

The seven possible pentomino shapes are shown below the grid. Their reflections or rotations would also be possible shapes. 

Puzzle of the Week #49 - Pair-of-Dice Regained

I have a pair of dice, which are numbered in an unconventional way. Unlike normal dice, where you can achieve a maximum total of 12, and often the same total can be achieved in several different ways, (eg 5+2=3+4=1+6=7, etc), these dice can total any number from 2 to 37 in exactly one way each.

All of the numbers on the dice are positive whole numbers, and one of the dice has four square numbers on it.

How are the dice numbered?